《XORing Elephants: Novel Erasure Codes for Big Data》论文翻译（arXiv:1301.3791v1）

本篇文章是对论文XORing Elephants: Novel Erasure Codes for Big Data的原创翻译，转载请严格遵守CC BY-NC-SA协议。

作者

Sathiamoorthy University of Southern California [email protected]

Megasthenis Asteris University of Southern California [email protected]

Dimitris Papailiopoulos University of Southern California [email protected]

Alexandros G. Dimakis University of Southern California [email protected]

Ramkumar Vadali Facebook [email protected]

Scott Chen Facebook [email protected]

Dhruba Borthakur Facebook [email protected]

摘要

大型分布式存储系统通常使用副本来提供可靠性。最近，为了减少三副本系统带来的巨大开销，开始使用纠删码。在设计时，一般选择Reed-Solomon码（RS码）作为标准，其高昂的修复开销往往被认为是为了高效存储和高可用性而带来的不可避免的代价。

本篇论文展示了如何克服这一限制。我们提出了一个新的擦除码族，它们可以高效修复并提供比RS码更高的可靠性。我们通过分析表明，我们的编码在权衡局部性和最短距离时能做出最优的决策。

我们在Hadoop HDFS中实现了我们的新的编码方式，并与当前部署的使用了RS码的HDFS模块做了比较。我们修改的HDFS实现在修复时减少了约2倍的磁盘I/O和网络流量。新的编码方案的缺点是在修复时需要修复比RS码多出14%的存储，这是从信息论角度为了获得部性最优的开销。因为我们新的编码方案能够更快地修复故障，因此其能够提供比副本的方式高几个数量级的可靠性。

1. 引言

MapReduce架构因其高伸缩性而在大数据管理中心变得越来越流行。在Facebook中，大型分析集群存储了PB级信息并使用Hadoop MapReduce处理很多的分析任务。其标准实现依赖一个通过利用了三副本的块来提供可靠性的分布式文件系统。副本策略的主要缺点在于其需要高达200%的额外存储开销，这一开销会反映在集群的开销上。当管理的数据快速增长时，这一开销会取代数据中心基础设施成为主要的瓶颈。

因此，Facebook和许多其他厂商正在切换到纠删码技术（通常指RS码）来在节约存储^{[4, 19]}的同时引入冗余，特别对于那些更像是归档的数据。在本文中，我们展示了传统的编码在分布式的MapReduce架构中离最优有很大差距。我们介绍了新的编码方式，以解决分布式系统可靠性和信息论约束的主要挑战，这也显示了我们的结构是最优的。本文依赖于对一个使用了Hadoop MapReduce来做数据分析的大型Facebook生产集群（超过3000个节点、30PB的逻辑数据存储）的测量。Facebook最近开始部署一个依赖RS码的叫做HDFS RAID^{[2, 8]}的开源HDFS模块。在HDFS RAID中，“cold（即很少被访问的）”文件的副本因子被降为1，并为其创建一个包含奇偶块的新的奇偶文件。

Facebook集群中使用的参数为，每个大文件的数据块被分组为10个条带（stripe），并对每个条带创建了4个奇偶校验块。太系统（被称为RS）可以容错任意4个块的故障，且其额外开销仅为40%。因此，RS码能提供比副本更强的健壮性和存储性能。事实上，该方案存储的额外开销对于该级别的可靠性来说是最小的^[7]。实现了这种最佳的存储和可靠性折衷的编码被称作是Maximum Distance Separable（MDS）^[31]的，RS码就^[27]是MDS族中被最广泛使用的编码方式。

传统的纠删码在分布式环境中不是最优的，这时由于修复问题（Repair problem）：当一个节点故障时，通常每个条带中被存储在该节点上的一个块会丢失。即使仅有一个块丢失，RS码通常会使用需要传输10个块并重建这10个数据块的原始数据的方式的简单方案来修复^[28]，这导致了在修复时产生了10倍的对带宽和磁盘I/O的额外负载。

最近，信息论的研究结果表明，和这种朴素方式^[6]相比，能够使用更少的网络带宽来修复纠错码。最近已经有大量关于设计这种高效的可修复的编码的工作，在第六章中有对这些文献的概览。

**我们的贡献：**我们介绍一个新的擦除码族——Locally Repairable Codes（LRCs），其可以在网络带宽和磁盘I/O方面进行高效修复。分析表明，我们的编码方案在局部性方面，从信息论的角度是最优的。即，修复单块故障所需的其他块数量是最优的。我们从广义的RS奇偶校验触发，提出了随机化和显式LRC结构的两种方案。

我们还设计并实现了HDFS-Xorbas，这是一个使用LRCs来替换HDFS-RAID模块中RS码的模块。我们通过使用Amazon EC2和一个Facebook中的集群的经验来评估HDFS-Xorbas。需要注意的是，尽管LRCCs可以在任何数量条带和任意大小的奇偶校验块上使用，我们的实验还是基于RS(10,4)和将其扩展到(10,6,5)的LRC与当前生产集群比较。

我们的实验表明，Xorbas比正在生产环境中使用的RS码大概减少了2倍的磁盘I/O和修复时的网络流量。这种新编码方案的缺点在于其需要比RS多14%的存储，为了获取局部性，这一开销从信息论的角度看已经是最优的了。

一个很有趣的好处是：Xorbas由于能在读取降级时提供更高效的性能表现，因此能够更快地修复故障，这提供了更高的可用性。在一个简单的Markov（马尔可夫）模型的评估下，Xorbas的平均数据丢失时间（Mean Time to Data Loss，MTTDL。译注：存储设备从运行开始到因故障导致数据永久丢失的平均时间）比RS(10,4)多了2个0，比3副本多了5个0。

1.1 修复的重要性

在Facebook，大型数据分析集群存储这PB级的数据并处理多个MapReduce分析任务。在有3000个节点的生产集群中存储了大概2亿2千万个块（每个块256MB），目前仅8%的数据正在使用RS编码（使用"RAID"）。图1展示了对这个生产集群中最近的节点故障的跟踪。即使在已经推迟大部分的修复任务以避免对暂时性故障进行不必要的修复的情况下，通常每天仍会有20个或更多的节点故障并触发修复任务。一个数据节点通常会存储约15TB的数据，在当前的集群配置下，其修复时需要的流量大概占集群每日网络流量（2PB/day）的10%到20%。就像我们之前讨论过的，(10,4)RS编码修复每位时需要比冗余块的方式多出10倍的网络流量。我们估计当集群中50%的数据使用RS编码时，其修复占用的网络流量会使集群的网络连接完全饱和。我们的目标是设计一个更高效的编码方案，使能够在不遇到修复瓶颈的情况下允许更高比例的数据使用该编码方案。这将会节约数PB的存储额外开销并能够大大较小集群的开销。

高效的可修复的编码方案在编码存储系统中变得越来越重要的原因还有4点。原因一，是读取降级（degraded read）问题。无永久性数据丢失的瞬时错误占数据中心错误事件的90%^{[9, 19]}。当瞬时性错误发生时，如果一个编码了的条带的相关数据块不可用时，对该块的读取会被降级（degraded）。在这种情况下，丢失的数据块可以被修复进程重建，其目的并不在于容错，而是为了更高的数据可用性。这与标准的数据修复的区别在于，为了可用性而重建的块不需要被写入磁盘。因此，高效且快速的修复可以大幅提高数据可用性。

原因二，是高效节点退役（node decommissioning）问题。Hadoop提供了退役特性来使一个故障的数据节点退出。在该节点退役前，需要将基本数据拷贝出该节点，这个过程复杂且耗时。快速修复像对待计划性的修复一样来对待节点退役的情况，并启动一个MapReduce任务在不造成大量网络流量的情况下重新创建块。

原因三，是修复操作对其它并发的MapReduce任务的影响。一些研究表明MapReduce的主要瓶颈是网络^[5]。正如我们提到的那样，修复占用的网络流量会在集群目前的网络带宽中占用客观的比例。使用的存储空间比数据中心的网络带宽增长得快得多，因此修复的网络占用问题会变得更加严重。存储密度的增长趋势让使用编码时能够局部修复变得更加重要。

最后，局部修复是促进跨数据中心的地理性（geographically）分布式文件系统的关键因素。多地（Geo-diversity）已被认为是未来改善时延和可靠性的关键方向之一^[13]。在传统方式中，站点通过副本的方式跨数据中心来分布式存储数据。然而，这种方式显著地增加了总存储开销。因为这种规模下跨地理位置的RS码需要大量的广域网带宽，所以这是完全不切实际的。我们的工作能在稍微提高存储额外开销的情况下使局部修复成为可能。

显然，采用副本的方式优化以上四个问题会更好，但是其需要更大的额外存储开销。相反，MDS码能够在给定的可靠性需求下使用最少的存储开销，但是会在修复方面和以上提到的问题中很困难。一种审视这篇文章的贡献的方式为：本文提出了该问题的一个新的中间权衡点，其牺牲了一定的存储效率以获取其他的指标。

本文的剩余部分按照以下方式组织：我们首先给出了我们的理论结果，即局部可修复编码（Locally Repairable Codes，LRC）的构造和从信息论角度的理论最优性结果。我们将更多技术性的证明放在了附录中。第三章展示了HDFS-Xorbas架构，第四章讨论了基于Markov的可靠性分析。第五章讨论了我们在Amazon EC2和Facebook中的集群的实验评估。最后，我们在第六章中调查了相关工作，并在第七章中进行了总结。

2. 理论贡献

极大距离可分码（Maximun distance sparable codes， MDS codes）经常在各种应用程序的通信和存储系统中被使用^[31]。一个比例为$R=\frac{k}{n}$的$(k,n-k)$-MDS码^注1将一个大小为$M$的文件划分为$k$个大小相等的块，并随后将其编码为$n$个每个大小为$\frac{M}{k}$的编码块。这里我们假设我们的文件大小和$k$个数据块的大小恰好相等以简化形式；大文件会被划分为多个条带，每个条带中有$k$个数据块，且每个条带都会被分别编码。

注1：在传统的编码理论文献中，编码被表示为$(n,k)$。其中$n$为数据块数量加奇偶校验块数量，通常被成为块长度（blocklength）。$(10,4)$RS码传统上被表示为RS$(n=14,k=10)$。所有RS码组成了最有名的MDS编码族。

$(k,n-k)$-MDS码可以保证$n$个编码块中的任意$k$个都可以被用来重建整个文件。易证，这是该冗余级别下可能实现的最佳容错条件：任意$k$个块的集合总大小为$M$，因此没有能够覆盖该文件的更小的块的集合。

容错能力可以通过最小距离这一指标来衡量。

定义 1 （最小编码距离，MINIMUM CODE DISTANCE）： 长度为$n$的编码的最小距离$d$，等于使文件不可恢复时，最少被擦除的块数。

顾名思义，MDS码有着能实现的最大距离，其$d_{MDS}=n-k+1$。例如，(10,4)RS的最小距离为$n-k+1=5$，这意味着想要数据丢失需要擦除5个或更多的块。

我们将关注的第二个指标为块的局部性。

定义 2 （块的局部性，BLOCK LOCALITY）： 当每个被编码的块是最多$r$个使用了该编码的其他被编码的块的函数时，那么这个$(k,n-k)$编码的块局部性为$r$。（译注：即对于一种编码，如果被编码的每个块都可以被最多$r$个使用了该编码的其他块通过运算表示，那么这个编码的局部性为$r$。）

有局部性$r$的编码有这样的属性：当任意一个块被擦除时，可以通过计算$r$个存在的使用该编码的块来快速修复丢失的编码块。这一概念最近在^{[10, 22, 24]}中引入。

当我们需要较小的局部性时，每一个编码块需要可以通过已存在的编码块的较小的子集来修复。即，即使$n$,$k$增大，仍需要$r \ll k$。以下事实显示了局部性和较好的距离冲突：

引理 1： 有参数$(k,n-k)$的MDS编码不能有比$k$更小的局部性。

引理1意味着MDS的局部性最差，因为其需要任意$k$个块才能重建整个文件，而不能仅重建一个块。即其局部性恰好是其最佳容错开销。

自然，我们需要解决的问题是：对于一个有着与MDS几乎相同的编码距离的编码，其可能的最佳局部性是多少。我们回答了这个问题，并构造了第一个有着高局部性的与MDS编码距离相近的编码族。我们提供了一个随机的和显式的编码族，其在所有的块上有对数的局部性，并有与MDS编码渐进相等的编码距离。我们称这些编码为$(k,n-k,r)$Locally Repairable Codes（LRCs，局部可修复编码），并在后续部分中介绍它们的构造。

定理 1： 存在$(k,n-k,r)$LRC，其有对数的块局部性$r=log(k)$，且编码距离$d_{LRC}=n-(1+\delta_{k})k+1$。因此，任何有$k(1+\delta_{k})$个编码块的子集都可被用来重建文件，其中$\delta_{k}=\frac{1}{log(k)}-\frac{1}{k}$。

显然，如果我们固定LRC的编码率$R=\frac{k}{n}$并增大$k$，那么其编码距离$d_{LRC}$几乎与$(k,n-k)$-MDS编码相同。因此有如下推论。

推论 1： 对于固定的编码率$R=\frac{k}{n}$，LRCs有着与$(k,n-k)$-MDS编码渐进相等的编码距离。

$$ \lim\limits_{k\to\infty}\frac{d_{LRC}}{d_{MDS}}=1 $$

LRCs构建在MDS编码之上（最常见的选择为RS码）。

将MDS编码的块分为对数大小的集合然后组合在一起后，可以得到有着对数的度（degree）的奇偶检验块。由于我们建立的信息论的权衡，我们证明了LRCs对给定的局部性有着最优的编码距离。我们的局部性-编码距离折衷十分普遍，因为其覆盖了线性编码和非线性编码，且其是对Gopalan等人最近的成果的推广^[10]，他们的成果为线性的编码建立了一个相似的边界。我们证明的方法基于建立了一个类似Dimakis等人的工作中信息流图^{[6, 7]}。我们的分析可在附录中找到。

2.1 Xorbas中LRC的实现

现在我们将描述我们在HDFS-Xorbas中实现的一个显式$(10,6,5)$LRC码。对于每个条带，我们从有10个数据块$X_{1},X_{2},…,X_{10}$并在二进制的扩展字段$\mathbb{F}{2^{m}}$上使用$(10,4)$RS码来构造4个奇偶校验块$P{1},P_{2},…,P_{4}$。这是目前在Facebook生产集群中使用的编码方案，由于RS奇偶校验，其可以容忍任意4个块的故障。LRCs的基本想法非常简单：通过增加额外的局部奇偶校验来使修复变得高效。我们通过图2展示了这一点。

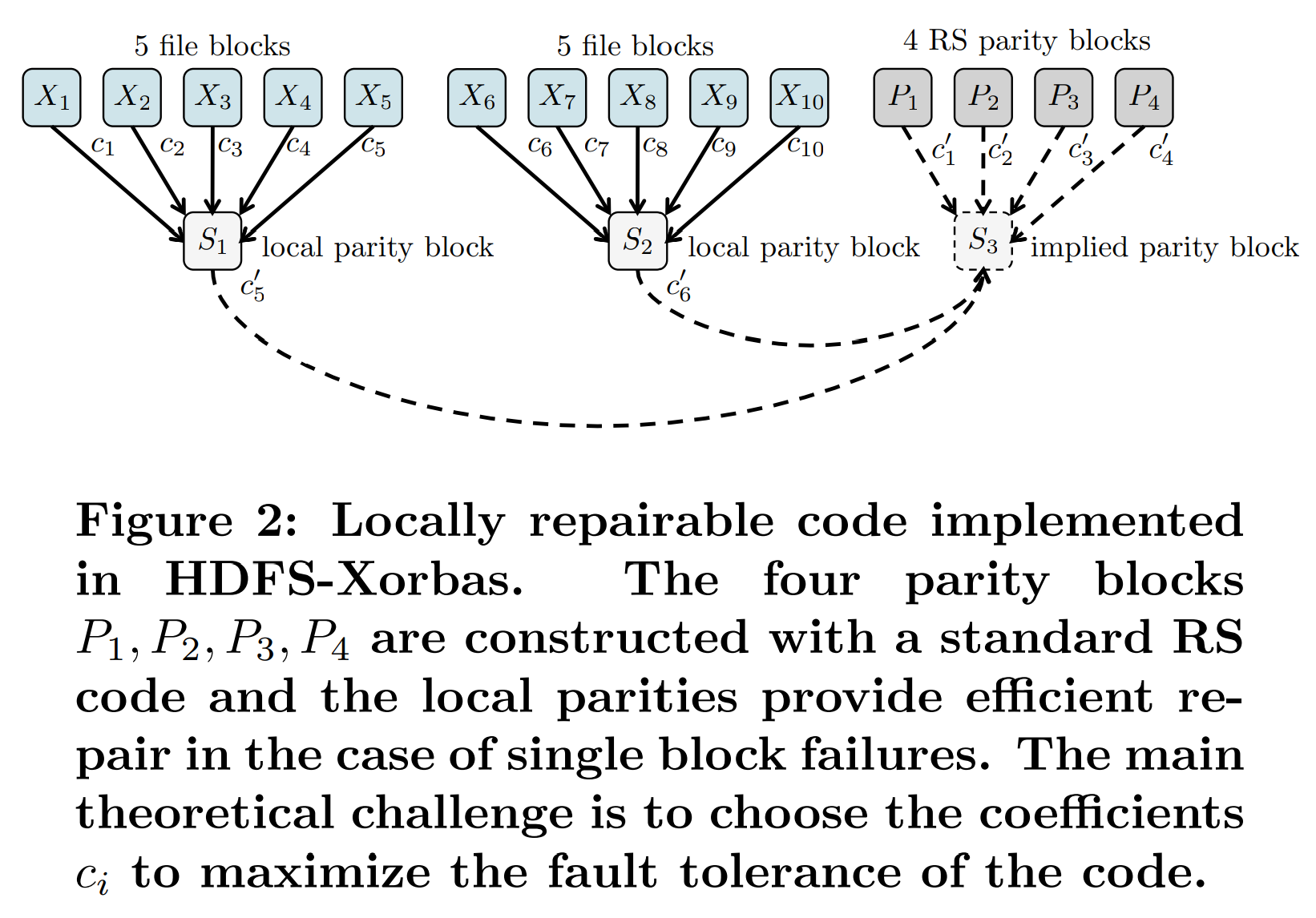
通过添加局部奇偶校验块$S_{1}=c_{1}X_{1}+c_{2}X_{2}+c_{3}X_{3}+c_{4}X_{4}+c_{5}X_{5}$，单块故障可以通过仅访问另外5个块来修复。例如，如果块$X_{3}$丢失（或在不可用时被读取降级）其可以通过下式重建。

$$X_{3}=c_{3}^{-1}(S_{1}-c_{1}X_{1}-c_{2}X_{2}-c_{4}X_{4}-c_{5}X_{5}) \tag {1}$$

只要$c_{3}$不为0其倒数就存在，这时我们对所有局部奇偶校验块的系数的要求。我们可以通过选择$c_{i}$使所有线性方程线性无关。在附录中我们提出了一个随机的和一个确定的算法来构建这些系数。需要强调的是，确定性的算法的复杂度与编码的参数$(n,k)$呈指数关系，因此其仅在小规模的编码构造中有用。

添加这些局部奇偶校验的缺点是需要额外的存储。原本使用RS码需要为每10个块存储14个块，而3个局部奇偶校验块将存储开销增加到了$17/10$。有一个额外优化我们可以实现：因此系数$c_{1},c_{2},…,c_{10}$可被选取，所以我们可以使局部奇偶检验块满足一个额外的校准方程$S1+S2+S3=0$。因此我们可以不存储局部奇偶校验块$S3$而将其看做是一个隐式奇偶校验块。需要注意的是，为了获得这一性质，我们需要置$c_{5} ’ +c_{6} ’ = 1$。

当RS奇偶校验块中的一个块发生故障时，可以重建隐式校验块并用其修复故障。例如，如果$P_{2}$丢失，可以通过读取$P_{1},P_{3},P_{4},S_{1},S_{2}$这5个块并通过如下等式来恢复该块。

$$ P_{2}=( c_{2} ’ )^{-1}(-S_{1}-S_{2}-c_{1} ’ P_{1}-c_{3} ’ P_{3}-c_{4} ’ P_{4}) \tag {2} $$

在我们的理论分析中，我们展示了如何找到能使条件成立的非零的系数$c_{i}$（其必须依赖$P_{i}$，但不依赖数据）。我们童颜展示了HDFS RAID中的RS码中的实现方式，其选择了$c_{i}=1 \forall i$，这是能够执行简单的XOR（异或）操作的充分条件。我们进一步证明了当给定局部性$r=5$且块长度$n=16$时的最大可行距离（$d=5$）。

3. 系统描述

HDFS-RAID是一个在Apache Hadoop^[2]上实现了RS编码和解码的开源模块。其提供了一个运行在HDFS之上的分布式RAID文件系统（Distributed Raid File System，DRFS）。存储在DRFS上的文件被划分为条带，即多个块的组。其对于每个条带都计算了一些奇偶校验块，且将其作为与原始文件对应的单独的奇偶校验文件存储。HDFS-RAID通过Java实现（大约12000行代码），且目前在包括Facebook的多个组织的生产环境中使用。

该模块由多个部件组成，其中最相关的是RaidNode和BlockFixer：

• RaidNode是负责创建和维护存储在DRFS中的所有数据文件的奇偶检验文件的守护进程。集群中的一个节点通常被设计为运行一个RaidNode。守护进程每隔一段时间会扫描HDFS文件系统并根据文件的大小和年龄来决定其是否需要使用RAID。在大型集群中，RAID是通过分布式的方式实现的，即将MapReduce任务分配给集群中的节点。在编码后，RaidNode会将使用了RAID的文件的副本等级降为1.

• BlockFixer是一个运行在RaidNode上的独立进程，其每个一段时间会使用了RAID的文件的丢失或损坏的块。当块被标记为丢失或损坏时，BlockFixer会使用其条带中幸存的块来重建它们，同样，这也是通过分配MapReduce修复任务实现的。需要注意的是，修复任务不是典型的MapReduce任务。修复任务是在MapReduce框架的下层实现的，其可以充分利用并行和调度属性，能够在一个控制机制下运行多个常规的任务。

RaidNode和BlockFixer都依赖下层组件ErasureCode。ErasureCode实现了纠错码（即擦除码）的编码和解码功能。在Facebook的HDFS-RAID中，我们通过ErasureCode实现了一个$(10,4)$RS纠错码（为每10个数据块创建4个奇偶校验块）。

3.1 HDFS-Xorbas

我们的系统HDFS-Xorbas（也简称为Xorbas）是基于HDFS-RAID的修改，其合并了LRC。为了便于它和HDFS-RAID中实现的RS码，我们称后者为HDFS-RS。Xorbas中继承了ErasureCode类，并在传统的RS码智商实现了LRC。为了利用新的编码方案，我们也对RaidNode和BlockFixer类做了修改。

HDFS-Xorbas被设计为可以在大型Hadoop数据仓库中部署，如Facebook的集群。为此，我们的系统提供了向后兼容性：Xorbas同时支持LRC和RS编码，且可以通过仅添加局部XOR奇偶校验文件的方式将RS编码的文件增量修改为LRC编码的文件。为了与HDFS-RS继承，我们使用的特定LRCs被设计为Facebook中使用的$(10,4)$RS码的扩展。首先，文件会被使用RS码编码，接着会为其创建提供局部修复能力的额外的局部奇偶校验块。

3.1.1 编码

一旦RaidNode（根据配置文件中设置的参数）检测到一个文件适合RAID，，它会启动该文件的编码器。编码器首先将文件划分为多个每个中有10个块的条带，并为其计算出4个RS奇偶校验块。其中，最后一个条带中可能包含少于10个块，这取决于文件的大小。对奇偶计算来说，不完整的条带会被看作是被0填充了的满的条带。

HDFS-Xorbas为每个条带的总计16个块计算2个额外的奇偶校验块（即10个数据块，4个RS奇偶校验块和2个局部XOR奇偶校验块），如图2所示。与RS奇偶校验块的计算类似，Xorbas通过分布式的方式计算所有的奇偶校验块，即MapReduce编码任务。所有的块会根据Hadoop中配置的块放置策略（block placement policy）被分散到集群中。默认的策略为随机将块放置到DataNode上，并避免同一条带上的块分配到同一个DataNode上。

3.1.2 解码与修复

当检测到损坏的文件时，RaidNode会启动一个解码进程。Xorbas使用了两个解码器：轻量级的解码器用来处理每个条带中单个块的故障，重量级的解码器会在轻量级解码器处理失败时被使用。

当BlockFixer检测到丢失（或损坏）的块时，它会根据LRC的结构决定使用哪5个块来重建该块。之后会分配一个特殊的MapReduce任务来进行轻量级的解码：单个map任务向包含所需的块的节点打开并发的流，并下载这些块，再执行一个简单的XOR操作。对于多块故障，所需的5个块可能不可用。在这种情况下，轻量级解码器会失败并启动重量级解码器。重量级解码器使用与RS相同的操作：打开对该条带所有块的流，并通过等价于解一个线性方程组的方式解码。RS线性系统具有Vandermonde（范德蒙）结构^[31]，这可以减少对CPU的利用。被恢复的块会按照集群块放置策略最终被发送并存储到一个Datanode中。

在当前部署的HDFS-RS的实现中，及时当仅有一个块损坏时，BlockFixer也会打开到该条带中其他的所有13个块的流（在更高效的实现中也可以将这个数量减少到10个）。因此，Xorbas的优势十分明显：对于所有单块故障和许多两个块故障（即两个丢失的块属于不同的局部XOR组中时）的情况，网络和磁盘I/O的开销会小的多。

4. 可靠性分析

在本章中，我们会通过标准的马尔科夫模型估算平均数据丢失时间（MTTDL）来提供可靠性分析。我们通过上述的指标和模型将RS、LRCs与副本的方式进行了对比。影响MTTDL的主要因素有两个： $i)$在数据丢失前我们能够容忍的故障块的数量和 $ii)$修复块的速度。容错能力越强，MTTDL越高，修复块所需的时间越短。接下来，我们将探索这些因素的相互影响及它们对MTTDL的影响。

在不同策略的对比中，副本策略能够在较低的容错开销下提供最快的修复速度。另一方面，RS码和LRCs能够容忍更多故障，但相比需要更长的修复时间，其中LRC比RS需要的修复时间短。在^[9]中，作者展示了Google集群中的数据，并报告说在他们的参数下，$(9,4)$-RS码能够提供比3副本策略高出约6个数量级的可靠性。同样，在这我们也将看到编码的方式如何在我们关注的可靠性方面由于副本策略。

正如^[9]中所述，目前有大量分析了副本、RAID存储^[32]和纠删码^[11]的可靠性的工作。这些文献的主要部分采用了标准的马尔科夫模型分析推导各种存储设置的MTTDL。和这些文献一样，我们也采用了一个类似的方法估算我们对比的策略的可靠性。这里得到的数据孤立地看可能没有意义，但在对比不同策略时非常有用（参见^[12]）。

在我们的分析中，$C$表示集群中总数据量，$S$表示条带大小。我们设磁盘节点数量$N=3000$，数据存储总量$C=30PB$。每个磁盘节点的平均故障时间为4年（$=1/ \lambda $），块大小$B=256MB$（Facebook数据仓库的默认值）。基于对Facebook集群的测量，我们限制修复时跨机架的通信速率$ \gamma = 1Gbps $。添加这一限的目的是模拟现实中Facebook集群跨机架通信的带宽限制。在我们的条件下，跨机架通信来自于同一个条带所有不同的编码块都被放置在了不同的机架上，以提高容错能力。这意味着当修复单个块时，参与修复的所有的块都会被从不同的机架下载。

在3副本策略下，每个条带由这三个副本的对应的三个块组成，因此系统中条带的总数量为$C/nB$，其中$n=3$。当使用RS码或LRC码时，条带的大小会根据编码的参数$k$和$n-k$变化。为了进行比较，我们认为每个数据条带大小$k$=10。因此，条带的数量为$C/nB$，其中对$(10,4)$RS来说$n=14$，对$(10,6,5)$-LRC来说$n=16$。对于以上值，我们计算单个条带的MTTDL（$MTTDL_{stripe}$）。随后，我们通过之前计算的总条带数对其归一化，得到系统的MTTDL，其计算方式如下。

$$ MTTDL = \frac{MTTDL_{stripe}}{C/nB} \tag {3} $$

接下来，我们解释如何计算一个条带的MTTDL，对其我们可以使用标准的马尔科夫模型。每次失去的块的数量用来表示马尔科夫链的不同状态。故障和修复率对应两个状态间的正向转移和反向转移概率。当我们使用3副本策略时，在3个块被擦除后会发生数据丢失。对于$(10,4)$-RS和$(10,6,5)$-LRC策略，5个块被擦除后会导致数据丢失。因此，以上存储场景的马尔科夫链分别总计有3、5、5个状态。在图3中，我们展示了$(10,4)$-RS和$(10,6,5)$-LRC对应的马尔科夫链。我们注意到，尽管这两个链有相同的状态数，但是状态转移概率会是不同的，其取决于编码策略。

我们接下来计算状态转移概率。假设发生故障的间隔时间呈指数分布。修复时间也是如此。通常，修复时间可能不服从指数分布，然而，这样假设可以简化我们的分析。当条带中还有$i$个块时（即，当状态为$n-1$时），失去一个块的概率$ \lambda _{i} = i \lambda $，因为这$i$个块分布在不同节点上，且每个节点故障事件是独立的，其概率为$\lambda$。块被修复的概率取决于修复需要下载多少个块、块大小和下载速率$\gamma$。例如，对于3副本策略，修复单个块需要下载一个块，因此我们假设$\rho _{i} = \gamma / B $，其中$i=1,2$。对于编码策略，我们需要额外考虑使用轻量级和重量级编码器的影响。以LRC为例，如果两个相同条带的块丢失，我们决定调用轻量级和重量级编码器的概率，然后计算需要下载的块数的期望。受篇幅所限，我们跳过详细的推导。相似的做法可参见^[9]。条带的MTTDL等于其从状态0到数据丢失状态的平均时间。在以上的假设和状态转移概率下，我们来计算条带的MTTDL，这样就可以通过**公式(3)**计算系统的MTTDL。

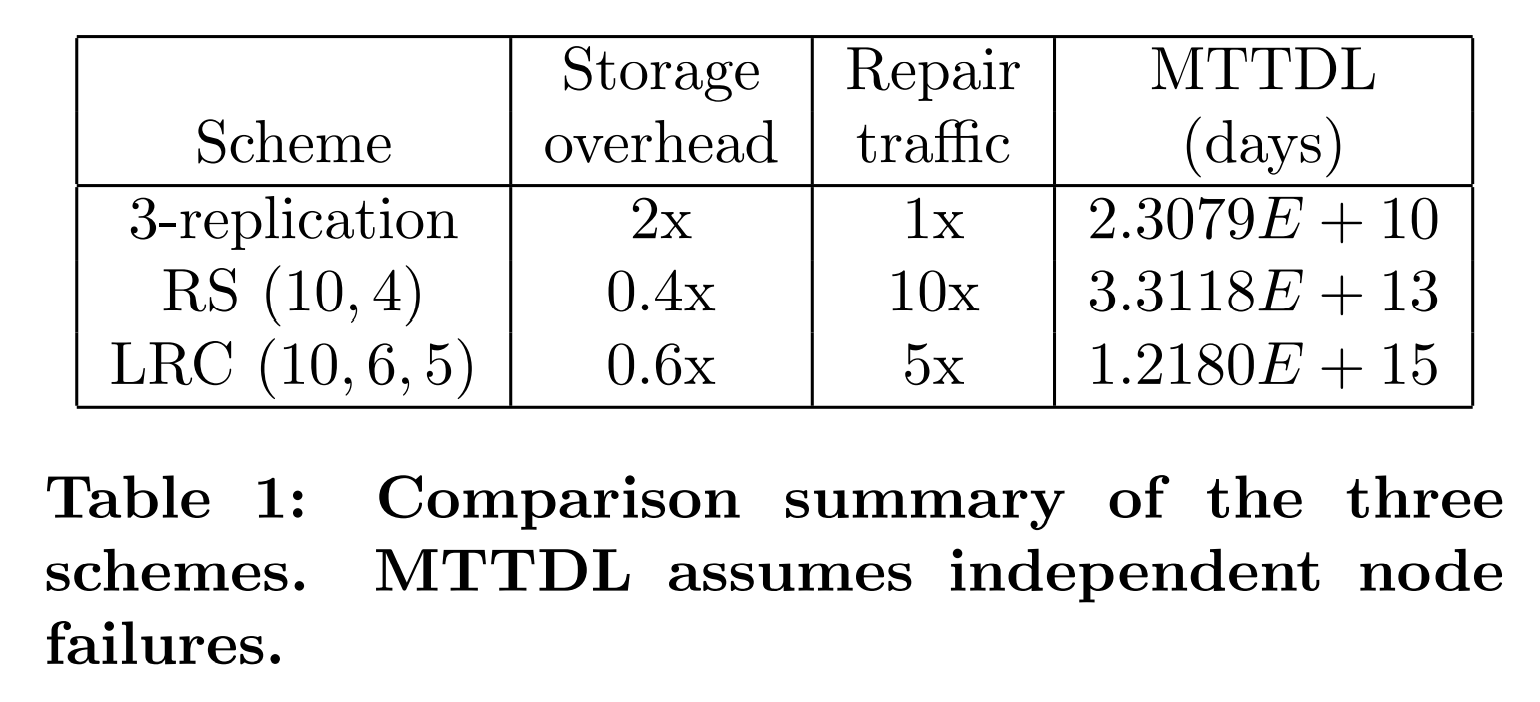
我们在马尔可夫模型下计算得到的副本策略、HDFS-RS和Xorbas的MTTDL的值如表1所示。我们观察到，在可靠性方面，LRC较高的修复速度弥补了需要额外存储的不足。这让Xorbas LRC$(10,6,5)$比$(10,6)$RS码的可靠性多出了两个0。三副本策略的可靠性比两种编码策略的可靠性低得多，这与相关工作^[9]中观测到的结果相似。

另一个有趣的指标是数据可用性。可用性是数据可用时间的比例。需要注意的是，在三副本策略中，如果一个块丢失，该块的其它副本之一会立刻变得可用。相反，无论对于RS还是LRC来说，需要丢失了块的任务必须等修复任务执行完成。因为LRCs在读取降级后读取速率相对更快，所以能更快地完成这些任务，因此它们有更高的可用性。对编码存储系统权衡可用性的详细研究仍是未来中有趣的研究方向。

5. 性能评估

在本章中，我们提供了我们为了在两个环境下（Amazon’s Elastic Compute Cloud (EC2)^[1] 和Facebook中的一个测试集群）评估HDFS-Xorbas的性能的而开展的一系列实验的详细情况。

5.1 评估指标

我们主要依赖以下指标来评估HDFS-Xorbas和HDFS-RS：HDFS读取字节数、网络流量和修复时间。HDFS读取字节数对应修复任务发起的总数据读取量。该值通过聚合故障事件后的任务分析报告的部分的测量值得到。网络流量代表了集群中节点间数据通信总量（按GB测量）。因为集群不处理任何额外的流量，所以网络流量等于了节点数据移动的总量。修复时间通过修复任务的开始时间和结束时间简单计算得到。

5.2 Amazon EC2

在EC2我们创建了两个Hadoop集群，其中一个运行HDFS-RS，另一个运行HDFS-Xorbas。每个集群由51个m1.small类型的实例组成，每个实例对应了一个32位机器，有1.7GB内存、1个计算单元、160GB的存储，运行着Ubuntu/Linux-2.6.32。每个集群中的1个实例作为master，运行着Hadoop的NameNode、JobTracker和RaidNode守护进程；剩下的50个实例作为HDFS和MapReduce的slave，每个实例上运行着一个DataNode和一个TaskTracker守护进程，从而形成了一个总容量约为7.4TB的Hadoop集群。不幸的是，EC2没有提供集群的拓扑信息。两个集群初始时装载了等量的逻辑数据。随后在两个集群中手动触发相同的故障模式，一眼就数据恢复的动态情况。实验目标是测量修复时如HDFS读取字节数、真实的网络流量等关键属性。

实验使用的所有文件大小都为640MB。块大小被配置为64MB，在HDFS-RS和HDFS-Xorbas中每个文件产生的每个条带中分别有14和16个满大小的块。这种选择代表了Hadoop生产集群中大部分条带的情况：非常大的文件被分成多个条带，因此大小较小的条带只占了总数中很小的比例。另外，这允许我们更好地预测为了重建丢失的块所需的总数据读取量，从而解释我们的实验结果。最后，因为快的修复仅依赖同一条带，使用会生成多个条带的大文件不会影响我们的结果。章节5.3中讨论了一个关于任意文件大小的实验。

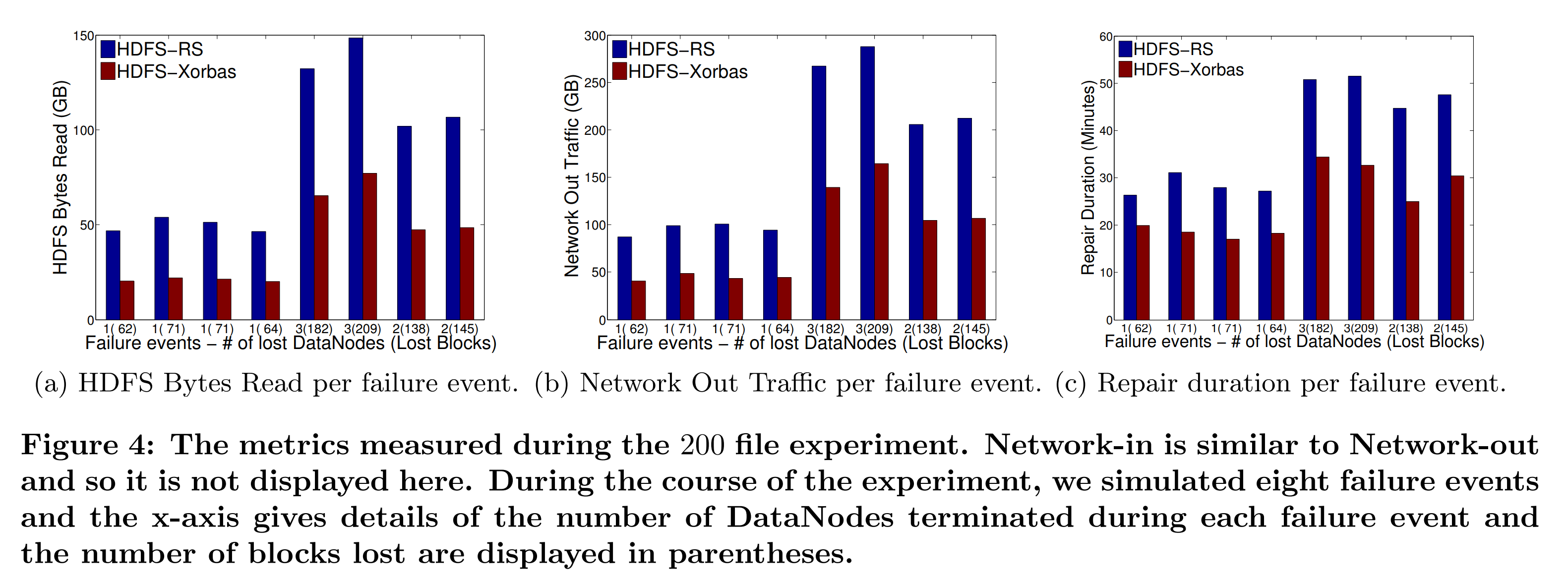
在一次实验期间，所有的文件都使用了RAID，每个集群中都出发了8次故障事件。故障事件包括杀死一个或多个DataNode运行。在我们的故障模式中，前4个故障事件中杀死了1个DataNode，接下来两个故障事件杀死了3个DataNode，最后两次杀死了两个DataNode。当故障事件发生时，RaidNode通过发起的MapReduce修复任务来恢复丢失的块。我们为两个集群提供了足够的时间来完成修复进程，以能对每个独立的事件进行测量。例如，图4中的事件是独立的。需要注意的是在两个集群中被选取杀死的DataNode种大概存储了相同数量的块。实验的目标是对比两个系统修复每个丢失的块的开销。然而，因为Xorbas有着额外的存储开销，一个随机的故障事件可能会导致Xorbas失去块的数量比RS多出14.3%。在任何情况下，对于考虑了这个开销的情形结果仍然适用，在我们的实验中不会观察到显著的影响。

为了了解数据量对系统性能的影响，我们在上述设置下进行了三个实验，依次增加存储的文件数量（50、100和200个文件）。图4中给出了最后一种条件下的测量结果，另外两次实验产生了类似的结果。所有实验的测量结果被合并在了图6中，其绘制了EC2中所有三次实验中的HDFS字节读取量、网络流量、修复时间与丢失的块的数量。我们还绘制了这些测量值的线性最小二乘拟合曲线。

5.2.1 HDFS字节读取数

图4a描述了在每次故障发生时由BlockFixer发起的HDFS字节读取总量。条形图表明，在重构相同数量的丢失的块时，HDFS-Xorbar的数据读取量为RS的41%~52%。考虑到每个块上很少有超过1个块丢失，这些测量值符合理论上的期望值（$12.14/5=41%$）。图6a展示了HDFS字节读取数与块丢失数的线性关系，这正与我们预期的一样。其斜率即为Xorbas和HDFS-RS中平均每个块读取的HDFS字节数。平均每个丢失的块读取的字节数估算的值分别为11.5和5.8，这表明了HDFS-Xorbas有2倍的优势。

5.2.2 网络流量

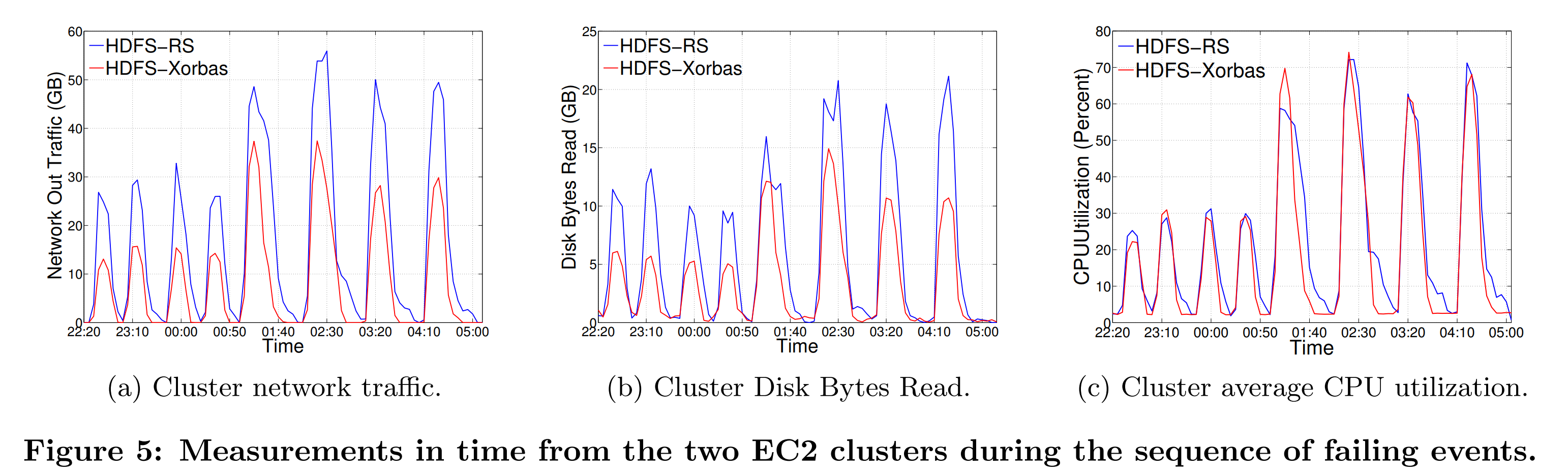
图4b描述了在整个修复过程中BlockFixer任务产生了网络流量。特别地，其展示了集群中所有实例的网络出流量的聚合。因为集群仅在内部通信，因此网络的出流量和入流量相似。在图5a中，我们展示了在200个文件的实验期间每5分钟的网络流量图。故障事件序列清晰可见。在我们整个实验中，我们始终都能观察到网络流量大概等于读取字节数的两倍。因此，正如我们预期的那样，HDFS读取的字节数的增加会转化为网络流量的增加。

5.2.3 修复时间

图4c描述了整个恢复过程的时间（即从第一个块的修复任务开始到最后一个块修复任务终止的时间 ）。图6c结合了所有实验中的测量值结果，其展示了修复时间和修复的块的数量的关系。这些图显示Xorbas完成时间比HDFS-RS快了25%~45%。

这两个系统的流量峰值不同的这一事实，表明了实验中可用的带宽没有完全饱和。在大规模MapReduce任务中^{[5, 14, 15]}，网络通常是瓶颈。在Facebook的生产集群中大规模修复发生时，也会观测到相似的情况。这是因为数百台机器可能共享同一个顶层交换机，且该交换机饱和了。由于LRC传输的数据量少得多，我们预计网络瓶颈会导致大规模的RS修复完成时间进一步推迟，也因此LRC在恢复时间上有比RS更大的优势。

从CPU利用率的图表中我们可以得出结论：HDFS-RS和Xorbas有着相似的CPU需求，且这似乎不会影响修复时间。

5.2.4 修复下的工作负载

为了掩饰修复的性能对集群负载的影响，我们在执行着其他任务的集群中模拟了块的丢失。我们创建了两个集群，每个包含了15个slave。由人工提交的工作负载包含5个在同一个3GB文本文件上运行的word-count工作（job）。每个工作（job）包含了许多任务（task），这些任务足以占据所有的计算槽（slot）。Hadoop的FairScheduler将任务分给TaskTracker使各个工作的计算时间能被公平地分享。图7描述了两种情形下每个工作的执行时间： $i)$所有被请求的块都可用，和 $ii)$请求的块的最多20%丢失。不可用的块必须在重建后才能被访问，这增加了任务完成的延时。在HDFS-Xorbas中，这个延时要小得多。在已进行过的实验中，RS中由于块丢失而导致的额外的延时比LRC的二倍还多（LRC中为9分钟，RS中为23分钟）。

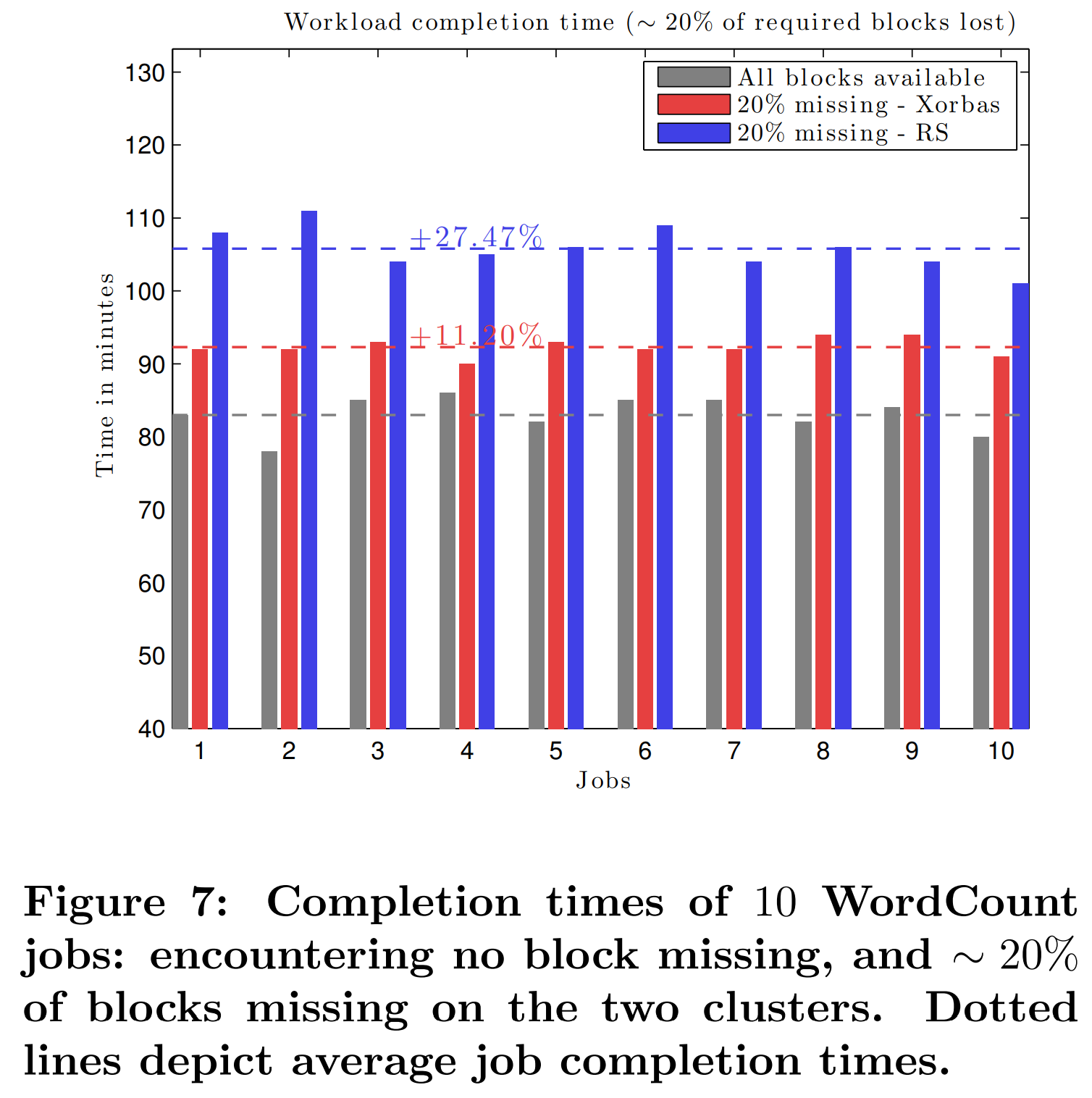
我们注意到，这些优势主要取决于Hadoop FairScheduler的配置方式。如果并发的工作被阻塞，但是调度器仍为他们分配了槽，那么延时会大幅增加。而且，修复时间超过阈值，那么需要读取块的工作可能会失败。在这些实验中，调度配置的选项是按照对RS最有利的方式设置的。最后，像之前讨论过的那样，由于网络饱和，我们预期在大规模的实验中，LRCs会比RS快的更多。

5.3 Facebook的集群

除了一系列在EC2上执行的受控的实验外，我们还在Facebook的测试机群上进行了另一个实验。测试集群由35个总容量为370TB的节点组成。我没没有像在EC2中那样在集群中预先放置确定大小的文件，而是直接利用了集群中现有的文件集：共3262个文件，总计约2.7TB的逻辑数据。块大小采用了256MB（与Facebook的生产集群相同）。大概94%的文件由3个块组成，其余的文件由10个块组成，即平均每个文件由3.4个块组成。

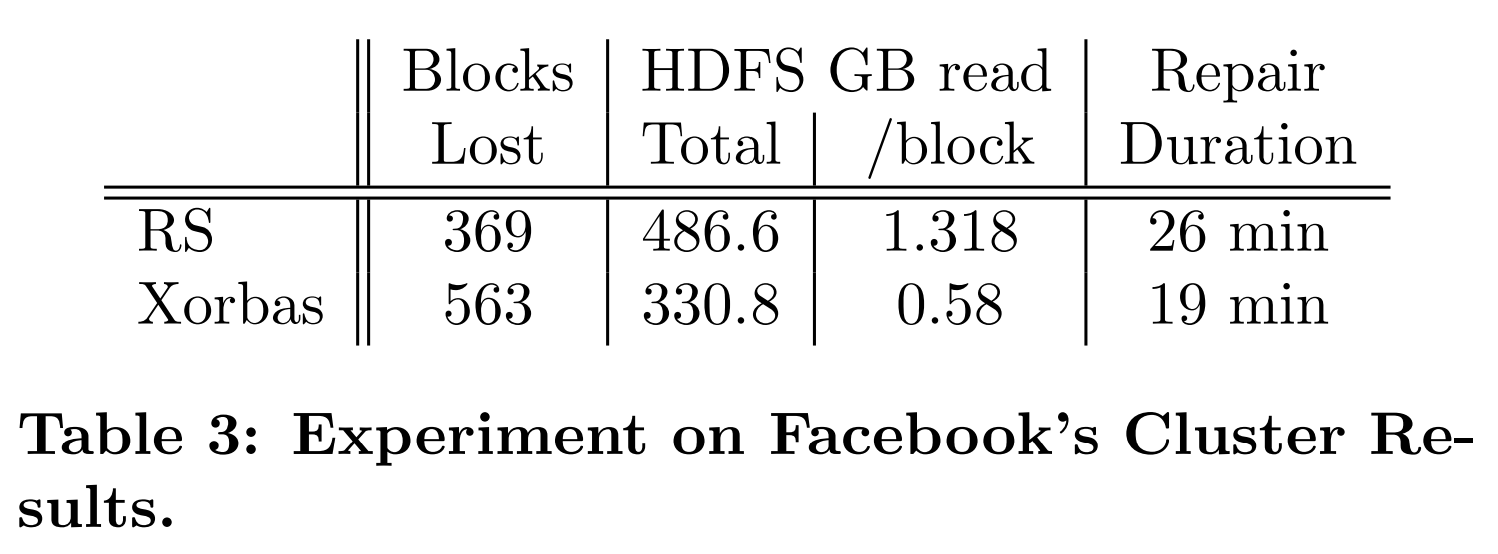
对我们的实验来说，集群上部署了HDFS-RS，且一旦数据的RAID操作完成后，就会有一台随机的DataNode被杀死。对HDFS字节读取量和修复时间的测量值会被采集起来。不幸的是，我们没有对网络流量的测量。实验会在以相同配置部署的HDFS-Xorbas上再次执行一遍。结果在表3中显示。需要注意的是，在本次实验中，HDFS-Xorbas比HDFS-RS的存储多出了27%（理想情况下，额外开销应为13%），这是由于集群中存储的主要是小文件。正如我们之前提到的那样，被存储在HDFS上的文件通常很大（小文件通常会被归档为较大的HAR文件）。此外，需要强调的是，本次实验中使用的特定的数据集接不代表Facebook生产集群中存储的数据集。

在本实验中，第二次运行中丢失的块数超过了第一次运行时丢失的数量，因为HDFS-Xorbas引入了额外的存储开销。然而，我们还是能够观测到其在整体数据读取和修复时间上的优势，当将丢失的块的数量归一化之后，这些收益会更加明显。

6. 相关工作

为了实现高效修复而需要的编码优化问题是最近备受关注的主题，因为其与分布式系统有关。这里面有大量的工作要做，这里我们只视图给出一个高层的高数。感兴趣的读者可以参考^[7]和其中的参考文献。

本文与文献^[7]的第一个重要区别是功能性（functional）和精确（exact）修复的区别。功能性修复的意思是，当一个块丢失时，会创建一个不同的块来维持编码中指定的$(n,k)$的容错能力。函数性修复的主要问题在于，当一个系统块丢失时，它会被一个奇偶校验块替代。当纠错码的全局容错能力仍为$n-k$时，读取一个块的操作会变为需要访问$k$个块。尽管这样可能对很少被读取的归档系统很有用，但是这不适合我们的工作负载。因此，我们仅对能精确修复的编码感兴趣，这样我们可以系统地维护编码。

Dimakis等人^[6]表明了通过比朴素的策略（读并传输$k$个块）更小的网络流量来修复是可行的。最初的再生成（regenerating）编码^[6]仅提供了功能性修复，匹配信息论边界点值的精确再生成编码的存在性仍是一个开放的问题。

随后，大量的工作（如^{[7, 25, 30]}和其中的参考文献）表明，精确修复是可行的，其符合信息论^[6]的边界限制。精确修复编码被分为低比例的（$k/n<1/2$）和高比例的（$k/n>1/2$）。对于低比例的精确修复编码（例如存储额外开销大于2倍的），最近已经发现了合并了再生成编码的优美的结构实现^{[26, 29]}。副本策略有三倍的存储开销，而我们的应用程序最感兴趣的是存储负载在1.4~1.8的策略，这与使用低比例的精确再生成编码相违背。

目前，我们对于高比例的精确修复编码的理解还不够完整。这一编码是否存在性曾一直是开放问题，直到两组团队^[3]分别独立使用了干扰对齐（Interference Alignment）（一种为无线信息论开发的渐进技术，其表明比例高于$1/2$的精确再生成编码时存在的）。不幸的是，这一构造只具有理论意义，因为其需要指数的字段大小却仅在渐进状态下才能表现良好。显式的高比例再生成编码是研究热点课题，但是目前我们还不知道有可实际构建的方法。这些编码的第二个问题是这些编码中很多都减小了修复时的网络流量，但是有更高的磁盘I/O开销。目前还不知道高磁盘I/O是否是必需的，也不知道是否存在可实现的同时有较小的磁盘I/O和修复流量的编码存在。

另一族对修复做出优化的编码致力于放宽MDS的要求来改进修复的磁盘I/O和网络带宽（如^{[17, 20, 10]}）。这些结构中使用了局部性（locality）这一指标，即重建一个丢失的块时需要读取的块的数量。我们介绍的这些编码在局部性方面是最优的，它们符合在^[10]中给出的边界。在我们最近的先做出的工作中^[23]，我们推广了这一边界，并证明了它符合信息论（例如，其也适用于线性和非线性的向量编码）。我们发现最优的局部性对于最优磁盘I/O或最优修复时网络流量来说不是必须的，这些量的基本联系仍是开放的问题。

本文的主要理论进步是：一个依赖RS全局奇偶校验的有最优局部性的心得编码结构。我们展示了隐式奇偶校验的概念如何节约存储，并展示了如果全局奇偶校验法是RS时，如何显式地实现奇偶校验校准。

7. 结论

现代存储系统转向了纠删码技术。我们介绍了一个叫做Locally Repairable Codes（LRCs）的新的编码族，其在存储方面略逊于最佳水平，但修复时磁盘I/O和网络带宽需求明显更小。在我们的实现中，我们观测到其减少了2倍的磁盘I/O，并仅需14%的额外存储开销，这一代价在很多场景下是合理的。

我们认为局部可修复编码能产生重大影响的相关领域是纯归档集群。在这一情况下，我们可以部署大型LRCs（即条带大小为50或100个块），其会同时提高容错能力并减小存储额外开销。因为修复所需的流量随条带的大小线性增长，因此在这一情况下使用RS码是不现实的。局部修复还会减少磁盘旋转^[21]，因为很少需要修复单个块。

总之，我们相信LRCs创建了一个新的操作点，其与大规模存储系统息息相关，特别是当网络带宽成为主要性能瓶颈时。

8. 参考文献

附录

附录A 通过熵的距离和局部性

接下来，我们将使用一个基于熵函数的长为$n$的编码的编码距离$d$的特征。这一特征非常普遍，其覆盖了任何线性和非线性的编码设计场景。

设我们希望将大小为$M$的文件划分为$x$份，并与$\frac{k}{n}$的冗余一起存在$n$个块中，每个块的大小为$\frac{M}{k}$。在不损失普遍性的情况下，我们假设文件被划分为了$k$个有相同大小$x \triangleq [X_1,…,X_k] \in \mathbb{F} ^{1 \times k}$的块，其中$\mathbb{F}$是所有被执行的运算的有限域。每个文件块的熵为$H(X_i)= \frac{M}{k}$，其中$i \in [k]$，$[n]= \lbrace 1,…,n \rbrace$^注2。接下来，我们定义编码（生成器）映射$G : \mathbb{F} ^ { 1 \times k} \mapsto \mathbb{F} ^ {1 \times n} $，其输入为$k$个文件块，输出$n$个编码块$G(x)=y=[Y_1,…,Y_n]$，其中对于所有$i \in [n]$，$H(Y_i) = \frac{M}{k}$。编码函数$G$在向量空间$\mathbb{F} ^{1 \times n}$上定义了一个$(k,n-k)$的编码$\mathcal{C}$。我们可以使用文件块的熵和$n$个编码块的熵之和的比值来计算编码的有效比例。

注2：换句话说，每个块被视作熵为$\frac{M}{k}$的随机变量。

$$ R = \frac{ H(X_1,…,X_k) }{ \sum _{i=1} ^{n} H(Y_i) } = \frac{k}{n} \tag {4} $$

编码$\mathcal{C}$的距离$d$等于擦除后剩余块的熵严格小于$M$的条件下的最小块擦除数量$y$。

$$ d= \mathop{min} \limits _{ H ( \lbrace Y_1,…,Y_n \rbrace \backslash \varepsilon ) < M } | \varepsilon | = n - \mathop{max} \limits _{ H(S) < M } | \mathcal{S} | \tag {5} $$

其中$ \varepsilon \in 2 ^{ \lbrace Y_1,…,Y_n \rbrace } $是块擦除模式的集合，且$ 2 ^{ \lbrace Y_1,…,Y_n \rbrace } $表示$\lbrace Y_1,…,Y_n \rbrace$的幂集，即该集合由所有的子集$\lbrace Y_1,…,Y_n \rbrace$组成。因此，对于一个长度为$n$，距离为$d$的编码$\mathcal{C}$，任意$n-d+1$个编码块都能重新构建该文件，即联合熵至少等于$M$。由此可知，当$d$给定时，$n-d$是使熵小于$M$的编码块最大数量。

编码的局部性$r$同样可以从编码块的熵的角度定义。当编码块$Y_i$，$i \in [n]$有局部性$r$时，那么对于另外$r$个编码块的变量有函数$Y_i=f_i(Y_{\mathcal{R}(i)})$，其中$\mathcal{R}(i)$索引了能重构$Y_i$的$r$个块的集合$Y_j$，$j \in \mathcal{R}(i) $，$f_i$是这$r$个编码块上的某个(线性或非线性)函数。因此，$Y_i$在其修复组$\mathcal{R}(i)$上的熵恒等于零，$H(Y_i|f_i(Y_{ \mathcal{R}(i) }))=0$，其中$i \in [n] $。$Y_i$对$\mathcal{R}(i)$的函数依赖基本上是在我们的推导中假设的唯一编码结构^注3。这种普遍性是为具有局部性$r$的线性或非线性的$(k,n-k)$编码提供通用的信息论边界的关键。接下来，在考虑局部性时，边界可以看做是编码距离的统一的辛格尔顿界（Singleton bound）。

注3：接下来，我们考虑有相同局部性的编码。即，$(k,n-k)$编码中所有编码块都有局部性$r$。这些编码被称为非规范化的编码^[10]。

附录B

才疏学浅… 后面实在翻不动了… 感兴趣的小伙伴请参考原文XORing Elephants: Novel Erasure Codes for Big Data。