《CRUSH: Controlled, Scalable, Decentralized Placement of Replicated Data》论文翻译

本篇文章是对论文CRUSH: Controlled, Scalable, Decentralized Placement of Replicated Data的原创翻译，转载请严格遵守CC BY-NC-SA协议。

作者

Sage A. Weil Scott A. Brandt Ethan L. Miller Carlos Maltzahn

Storage Systems Research Center

University of California, Santa Cruz

{sage, scott, elm, carlosm}@cs.ucsc.edu

摘要

新兴的大型分布式存储系统面临着将PB级的数据分布到数十、数百、甚至数千个存储设备上的问题。这样的系统必须均匀地分布数据和负载，以高效地利用可用资源并最大化系统性能，同时帮助处理增长并管理硬件故障。我们开发了CRUSH，一个可伸缩的伪随机数据分布函数，其为分布式对象存储系统设计，能高效地将数据对象映射到存储设备上，且而不依赖中央目录。因为大型系统有着固有的（inherently）动态性（译注：在Ceph中我将其翻译为“xxx本质上具有动态性”，本文中均翻译为“xxx具有固有的动态性”，以便于表达），CRUSh是为在帮助处理存储的增加与移除的同时减小不必要的数据移动而设计的。该算法适用于很多种类的数据副本和可靠性机制，同时根据用户定义的策略分布数据，这些策略可以强制将不同的副本分散到不同的故障域（failure domain）中。

1. 引言

对象存储是一种新兴的架构，它可以改善可管理性、可伸缩性和性能[Azagury et al. 2003]。与传统的基于块的硬盘驱动器不同，对象存储设备（object-based storage device，OSD）在内部管理磁盘块的分配，暴露可以让其它设备读取或写入到边长、命名对象的接口。在这种系统中，每个文件的数据通常会分条（strip）到数量相对少的命名对象中，而命名对象会分布在整个集群中。对象在有多个在多个设备上的副本（或者采用某些其他的数据冗余策略），以防止故障发生时数据丢失。基于对象的存储系统通过用较小的对象列表替代较大的块列表，以简化数据布局并分摊下层的块分配问题。虽然这通过减少了文件分配的元数据和复杂性大大提高了可伸缩性，但是将数据分布到数千个存储设备上（通常其容量和性能都不同）这一基本问题仍然存在。

大部分系统简单地将新数据写入到未被充分利用的设备上。这种方法的根本问题是，当数据被写入后，它很少甚至不会被移动。即使是完美的分布也会在存储系统被扩展后变得不均衡，因为新的磁盘或者是空的或者仅含有新的数据。旧的磁盘和新的磁盘可能都是繁忙的，这取决于系统负载，但是这很少能够平等地利用二者并得到所有可用资源的优势。

一种健壮的解决方案是将所有数据随机分布到系统中可用的存储设备上。这样可以使分布在概率上是均衡的，且新数据和旧数据会均匀地混合在一起。当添加新的存储时，已有数据的中的一份随机采样会被迁移到新的存储设备上以保持平衡。这种方法最重要的优势是平均，所有设备将会有相似的负载，让系统在任何潜在负载下表现良好[Santos et al. 2000]。另外，在大型存储系统中，一个大文件会被随机的分布到很多个可用的设备上，这可以提供很高的并行性和整体带宽。然而，简单的基于哈希的分布方法无法很好应对设备数量变化的情况，它会导致数据大量重新调配（reshuffle）。此外，已有的随机分布策略会将每个磁盘上的副本分散到许多其它设备上，它在多个设备同时故障时由很大的数据丢失的可能性。

我们开发了CRUSH（Controlled Replication Under Scalable Hashing，基于可伸缩哈希的受控多副本策略），它是一个伪随机数据分布算法，它能够高效、健壮地将对象副本在异构、结构化存储集群上分布。CRUSH的实现是一个伪随机、确定性的函数，它将输入值（通常是一个对象或对象组的标识符）映射到一系列存储对象副本的设备上。它与传统方法的不同点在于，它的数据分配不依赖每个文件或每个对象的任何类型的目录——CRUSH仅需要对构成存储集群的设备的紧凑的层次结构的描述和副本分配策略的知识。这种方法有两个关键的好处：第一，它完全是分布式的，大型系统中的任意一方都能单独计算任何对象的位置；第二，所需的元数据很少且几乎是静态的，它仅在有设备加入或移除时变化。

CRUSH是为优化数据分布以利用可用资源、在增加或移除存储设备时高效重新组织数据、和为数据副本分配提供灵活的约束以在意外或相关硬件故障时增加数据安全性设计的。其支持很多种数据安全机制，包括n路副本（镜像）、RAID奇偶校验策略或其它纠删码格式、和混合方法（例如RAID-10）。这些特性让CRUSH可以很好地适用于在可伸缩性、性能、和可靠性很重要的大型存储系统中（数PB）管理对象分布。

2. 相关工作

对象存储最近作为一种提高存储系统可伸缩性的机制备受关注。许多研究和生产级文件系统都采用了基于对象的方法，这包括影响深远的NASD文件系统[Gobioff et al. 1997]、Panasas文件系统[Nagle et al. 2004]、Lustre[Braam 2004]、和其它等基于对象的文件系统[Rodeh and Teperman 2003; Ghemawat et al. 2003]。其它的基于块的分布式文件系统像GPFS[Schmuck and Haskin 2002]和Federated Array of Bricks（FAB）[Saito et al. 2004]面临着类似的数据分布问题。这些系统使用了半随机（semi-random）或基于启发式（heuristic-based）的方法来将新数据分配到有可用容量的存储设备上，但是很少将数据重新放置以随着时间维护均衡的分布。更重要的是，所有的这些系统都通过某种元数据目录的方式定位数据，相反，CRUSH依赖紧凑集群描述（compact cluster description）和确定性映射函数（deterministic mapping function）。二者在写入数据时的区别最明显，使用CRUSH的系统不需要咨询中央分配器（central allocator）就能计算出任何新数据的存储位置。Sorrento[Tang et al. 2004]存储系统使用的一致性哈希[Karger et al. 1997] 与CRUSH最相似，但是其不支持设备权重控制（controlled weighting of devices）、数据良好均匀分布（well-balanced distribution of data）、和用来提供安全性的故障域（failure domains）。

尽管数据迁移问题已经在有显式分配映射的系统中有大量的研究[Anderson et al. 2001; Anderson et al. 2002]，这种方法对元数据的要求很高，而像CRUSH等方法想避免这一点。Choy等人[1996]描述了再次攀上分布数据的算法，其在磁盘增加时可以移动一定数量的对象以获得优化，但是不支持权重、副本、或磁盘移除。Brinkmann等人[2000]使用了哈希函数来将数据分布到异构但静态的集群中。SCADDAR[Goel et al. 2002]解决了添加或移除存储的问题，但是仅支持副本策略的一个受限的子集。这些方法都没有CRUSH的灵活性或用来提高可靠性的故障域的概念。

CRUSH基于RUSH算法族[Honicky and Miller 2004]且与其最为相似。RUSH是已有的文献中唯一的一个利用映射函数替代显式元数据并支持高效的加权设备添加或移除的算法。尽管RUSH算法有这些特性，但是大量的问题使其无法实际应用。CRUSH完整地包括了RUSH_P和RUSH_T中好用的元素，同时解决了之前未解决的可靠性和副本问题，并优化了性能和灵活性。

3. CRUSH算法

CRUSH算法参考每个设备的权重值来将数据对象从概率上近似均匀地分布到存储设备上。该分布受分层的（hierarchical）集群映射（cluster map） 控制，其表示可用的存储资源，由这些资源组成的逻辑元素构成。例如，人们可能通过如下方式描述一个大型设施（installation）：设施由多行服务器的cabinet（机箱架）组成，cabinet中装满了disk of shelf（磁盘柜，译注：下文中省略为shelf），shelf中装满了storage device（存储设备，译注，下文中省略为device）。数据分布策略是根据放置规则（placement rules） 定义的，这些规则指定了有多少目标副本被从集群中选取且副本放置时有哪些限制。例如，用户可能指定三份副本需要被放置在不同cabinet上的物理机上，这样它们就不会共享同一个电路。

给定一个整型输入值$x$，CRUSH会输出一个由$n$个不同的目标存储组成的有序列表$\overrightarrow{R}$。CRUSH使用了一个强大的多输入整型哈希函数，$x$是其输入之一，该函数可以使映射完全是确定性的，且可以仅通过集群映射、放置规则、和$x$计算。该分布是伪随机的，因为相似数据的输出结果或存储在任何device上的item（项）间没有明显的关联。CRUSH生成的副本分布是分簇（declustered） 的，因为一个item的副本所在的device与所有其它item的副本所在位置看上去也是独立的。

3.1 分层集群映射

集群映射由device 和bucket（桶） 组成，二者都有相关的数字型标识符和权重。bucket可以包括任意数量的device或其它的bucket，因此bucket可以在存储层次中作为中间节点，而device永远都是叶子节点。管理员为device分配权重，以控制它们负责存储的数据的相对的量。尽管大型系统很可能有不同容量、不同性能特征的device，但在随机的数据分布中，从统计学的角度看，device的利用率和负载相关，因此device的负载与存储的数据量成正比。因此，一维的放置矩阵（即权重）应从device容量推导得出。bucket的权重被定义为它包含的item的权重的和。

bucket可被随意组合来构建表示可用存储的层次结构。例如，用户可以创建如下的集群映射：在最下层使用“shelf（机柜）”来表示被安装的相同的device的集合，然后将多个“shelf”合并为“cabinet（cabinet）”bucket来将安装在同一个rack（机架）上的组合在一起。在更大的系统中，“cabinet”可能被进一步组合成“row（行）”或“room（房间）” bucket。数据通过一个伪随机类哈希函数在层次结构中递归选取嵌套的bucket item来放置。在传统的哈希技术中，对目标容器（device）数量的任何变更都会导致大量的容器内容重新调配；相反，CRUSH基于4种不同的bucket类型，每种类型都有不同的选取算法来解决device增加或移除带来的数据移动问题和整体的计算复杂度。

3.2 副本放置

CRUSH旨在将数据均匀地分布到加权的device上，以维护存储和device带宽资源的利用率在统计上的均衡。副本在层级结构中的device上的放置方式同样对数据安全性有重要影响。CRUSH可以反映出设施的物理组织方式，并通过它对潜在的“关联（correlated）设备故障源”建模，并解决这些问题。典型的关联设备源包括共享的电源、和共享的网络。通过将这一信息编码到集群映射中，CRUSH放置策略可以在维护所需的分布同时将对象的副本分散到不同的故障域中。例如，为了解决可能发生的关联故障，可能需要确保数据副本分布在不同的cabinet、rack、电源、控制器、和/或物理位置上。

为了适配各种可能使用CRUSH的场景，无论是在数据副本策略还是在底层硬件配置方面，CRUSH为采用的每个副本策或分部策略都定义了放置规则，这让存储系统或管理员可以精确地指定对象副本如何放置。例如，为一条选取了2个目标的规则采用2路镜像、为一条选取了3个在不同数据中心的的目标的规则采用3路镜像、为一条规则在5个device上采用RAID-4，等等^注1。

注1：尽管各种各样的数据冗余机制都是可行的，为了简单起见，我们提到的数据对象都被采用副本策略存储。

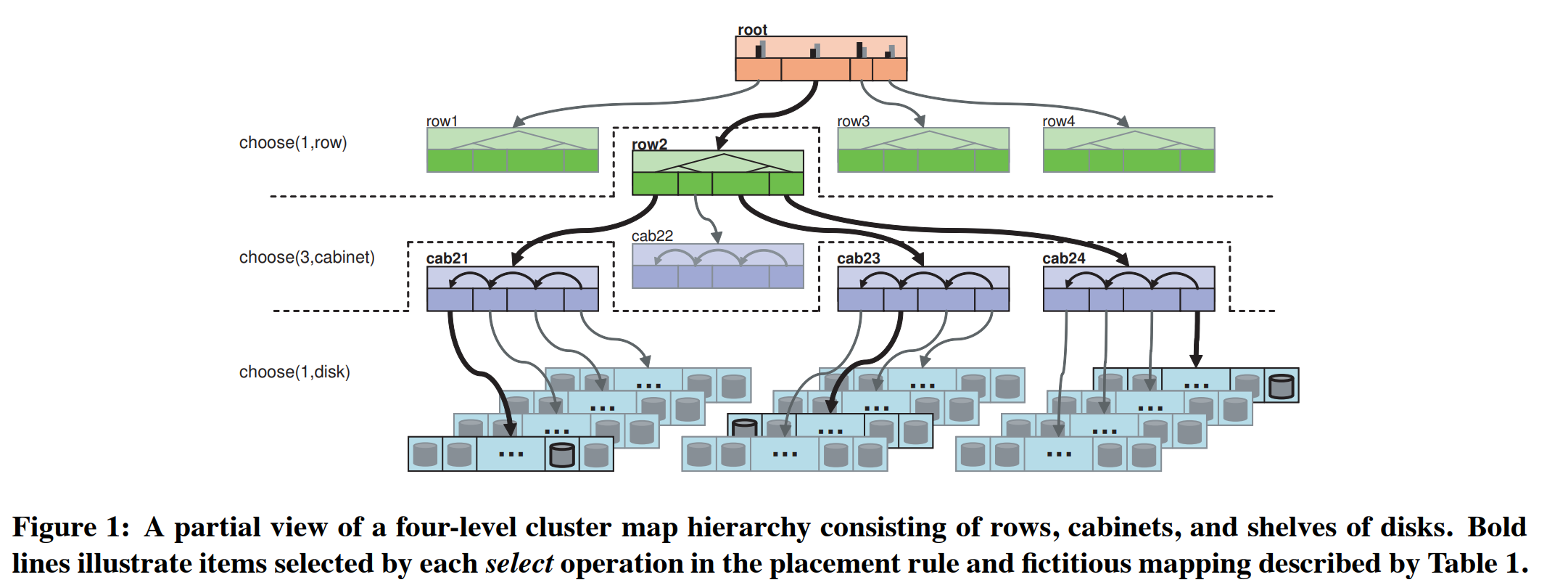
每条规则由一系列应用到层次结构中的简单操作组成，如算法1中的伪代码表示的那样。CRUSH函数的整型输入$x$通常是对象名或其它的标识符，如一组副本被放在同一个device上的对象的标识符。$take(a)$操作会在存储层次结构中选取一个item（通常是一个bucket），并将其分配给向量$\overrightarrow{i}$，作为后续操作的输入。$select(n,t)$操作遍历每个元素$i$（$i \in \overrightarrow{i}$），并在以该点为根的子树中选取$n$个类型为$t$的不同的item。device的类型已知且固定，且系统中的每个bucket都有一个类型字段，以用来区分不同类型的bucket（例如，用来表示“row”的bucket和用来表示“cabinet”的bucket）。对于每个$i$（$i \in \overrightarrow{i}$），$select(n,t)$调用会遍历item$r$（$ r \in 1,…,n $），并递归下降地处理中间的任何bucket，然后在每个bucket中通过函数$c(r,x)$（在章节3.4中为每类bucket定义的）伪随机地选取一个其中的item，直到它找到一个类型为请求的类型$t$的item。其产生的$n| \overrightarrow{i} |$个不同的item会被放回到输入$ \overrightarrow{i} $中，它们或作为后续$select(n,t)$的输入，或通过$emit$操作被移动到结果向量中。

例如，表1中定义的规则从图1中的层次结构的根开始。第一个$select(1,row)$选取了一个类型为“row”的bucket（其选取了row2）。随后的$select(3,cabinet)$在之前选取的row2内选择了3个不同的cabinet（cab21、cab23、cab24），最后，每个$select(1,disk)$遍历其输入向量中的3个cabinet bucket之一，并选择其下的1个disk。最终结果是分散在3个cabinet中的3个disk，但是都在同一个row中。因此，这种方法让副本能跨副本分布且对容器类型（例如，row、cabinet、shelf）进行约束，这一性质兼顾了可靠性和性能。规则由多个$take$、$emit$块组成，允许从不同的存储池中显式地提取目标存储，就像远程副本场景期望的那样（副本被存储在一个远程站点中）或分层设施场景期望的那样（例如，有快速近线存储和较慢但容量更大的存储阵列）。

3.2.1 碰撞、故障与过载

$select(n,t)$操作可能从它的起始点开始穿过多个存储层级以找到其下的$n$个不同的类型为$t$的item，它是一个以$r$（$r=1,…n$，n是所选的副本编号）作为部分参数的递归过程。在此过程中，CRUSH可能因三个不同原因拒绝（reject）并重新选取（reselect）item并修改输入$r’$：如果item已经被选取到当前的集合中（碰撞——$select(n,t)$的结果必须是不重复的），如果device是故障的（failed），或者如果device是过载的（overloaded）。故障或过载的device会在集群映射中标记出来，但这些device还留在层级结构中，以避免不必要的数据迁移。CRUSH会有选择地迁移一个过载device上的数据，这通过按集群映射中指定的概率伪随机地拒绝（reject）实现——这通常与device报告的过度利用的情况有关。对于故障或过载的device，CRUSH会重新开始$select(n,t)$开始处的递归（见算法1第11行），均匀地将它们的item分布到存储集群中。如果发生碰撞，在递归的内层尝试本地搜索时首先会使用$r’$（见算法1第14行）并避免整体数据分布偏离更可能发生冲突的子树（例如，bucket数小于n的子树）。

3.2.2 副本排名

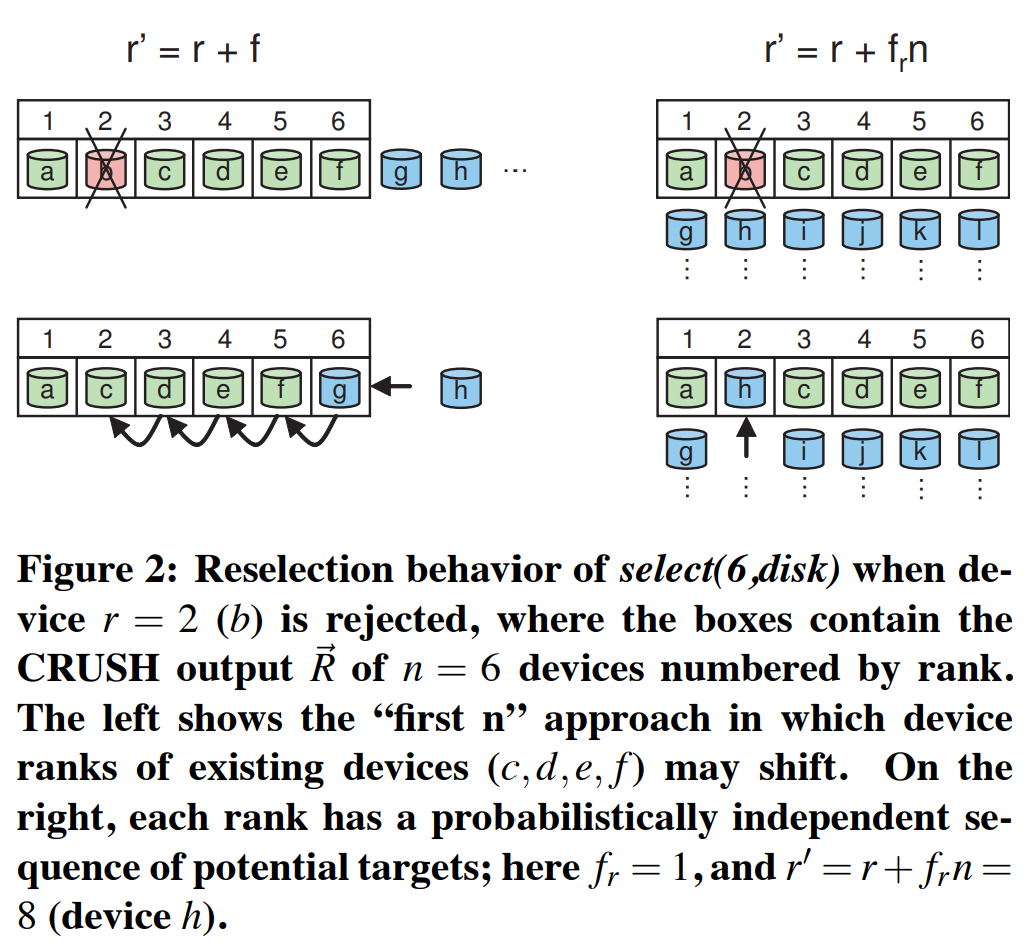
奇偶校验和纠删码策略与副本策略相比有明显不同的放置需求。在主拷贝副本策略（primary copy replication scheme）中，副本常常希望在之前的目标副本（已经有一份数据拷贝的副本）故障后成为新的主副本。在这种情况下，CRUSH可以用$ r ’ = r + f $来重新选取“前n个”合适的目标，其中$f$是当前的$select(n,t)$的失败的放置尝试次数（见算法1第16行）。然而，在奇偶校验或纠删码策略下，CRUSH输出中的device的排名或位置十分重要，因为每个目标保存数据对象的不同的位。特别是，如果一个device故障，CRUSH的输出列表$\overrightarrow{R}$的适当位置的item需要被替换，这样，列表中的其他device会保持相同的排名（即，$\overrightarrow{R}$中的位置，见图2）。在这种情况下，CRUSH会使用$ r ’ = r + f_{r} n $重新选取，其中$f_{r}$是在item$r$上的失败尝试的次数。因此，这为每个副本的排名定义了一个候选序列，每个候选序列从概率上与其它device的故障无关。相反，RUSH没有特殊处理device故障。像其它已有的哈希分布函数一样，它隐式假设使用“前n个”方法跳过结果中的故障device，这使其也适用于副本策略。

3.3 映射变更和数据移动

大型文件系统中数据分布的一个重要要素是对存储资源增加或移除的响应方式。CRUSH在所有时刻都会维护一个均匀的数据分布和负载，以避免负载不对称和相关可用资源利用不充分。当一个device故障时，CRUSH会标记该device，但仍将其留在层次结构中，这样它会被拒绝且它的内容会通过放置算法（见章节3.2.1）被均匀地重分布。这种集群映射的变化将会让总数据的最优（最小）比例（$ w_{failed} / W $，其中$W$是所有设备的总权重）被重新映射到新的存储目标上，因为仅故障设备上的数据会被移动。

当集群层次结构被改变时（例如增加或移除存储资源），情况会更加复杂。CRUSH的映射过程使用集群映射作为加权分层决策树，在这样的情况下可能造成比理论最优$ \frac{ \Delta w}{W} $更多的数据移动。在层次结构中的每一层中，当相对子树的权重变化改变了分布时，一些数据必须从权重减小的子树移动到权重增大的子树上。因为层次结构上的每个节点的伪随机放置决策在统计上是独立的，移动到子树的数据会在该点下均匀地重分布，但是不一定会被重新映射到导致权重变化的item下（译注：因此会造成更多的数据移动）。仅后面（更深）的层级的放置过程（经常是不同的）会移动数据以保持整体相对分布的正确性。图3中二分层级结构中说明了这种一般性的影响。

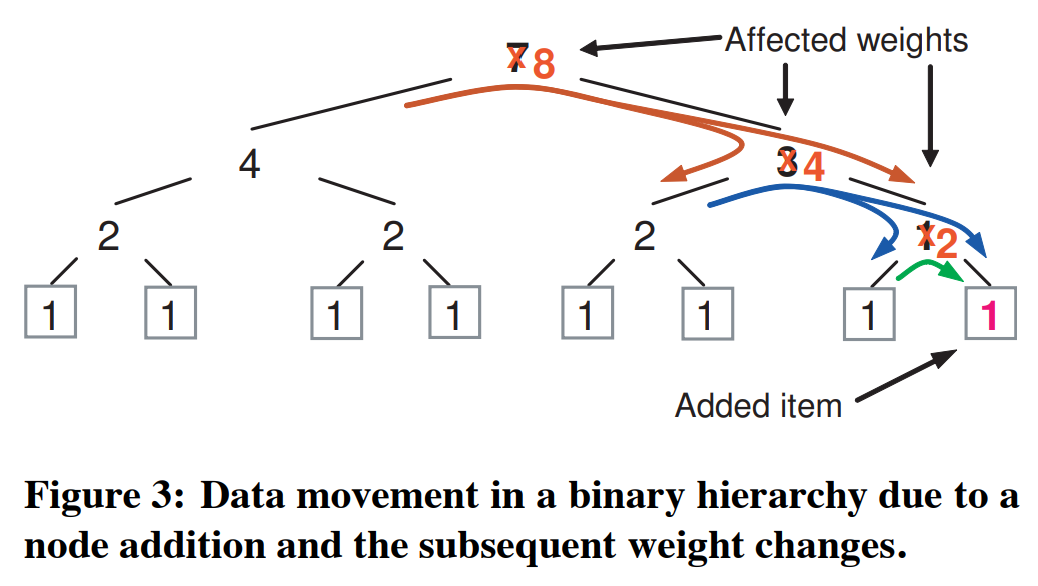
层次结构上的总数据移动量的下界为$ \frac{ \Delta w}{W} $，这是将驻留在权重为$ \Delta w$的新增device上的数据比例。数据移动量随着层次结构的高度$h$增长，其具有保守（conservative）的渐近上限$ h \frac{ \Delta w}{W} $。当$ \Delta w $比$W$小得多时，数据迁移的总量趋近于上界，因为在递归的每一步中移动到子树的数据对象被映射到权值相对小的item上的可能性很小。

3.4 bucket类型

通俗的说，CRUSH旨在调和两个互相竞争的目标：映射算法的性能和可伸缩性、在集群因增加或移除device变化时减小为恢复分布平衡的数据迁移量。为此，CRUSH定义了4个不同的bucket类型来表示集群层级结构的内部节点（非叶子节点）：uniform bucket、list bucket、tree bucket、straw bucket。每种不同的bucket类型都基于不同的内部数据结构，并在副本放置过程中使用不同的函数$c(r,x)$来伪随机地选择内部item，以表示在计算和重组织性能间不同的平衡点（tradeoff）。uniform bucket包含的item必须全都有相同的权重（很像常规的基于哈希的分布函数），而其它类型的bucket的item的权重可以不同。表2中总结了这些区别。

3.4.1 uniform bucket

device很少被单独添加到大型系统中。相反，新的存储通常以多个设备组成的一整块部署，例如在服务器rack中添加一个shelf或者可能添加一整个cabinet。达到寿命的device也经常作为一个集合退役（单独的设备故障除外），我们很自然地会视它们为一个整体。CRUSH的uniform bucket被用来表示这种情况下的一个相同的device的集合。其关键的优势在于与它的性能：CRUSH可以在恒定的时间内将副本映射到bucket中。在不适合使用均衡限制的情况中，可以使用其它bucket类型。

给定CRUSH的输入$x$和一个副本编号$r$，我们使用函数$c(r,x)=(hash(x)+rp) \mod m$从大小为$m$的uniform bucket中选择一个item，其中$p$是随机选择的（但是是确定的）大于$m$的质数。对于任意的$r \le m $，我们总是能使用一些简单的数论定理^注2来选择一个不同的item。对于$r > m$，这一保障不再成立，这意味着两个不同的副本$r$和相同的输入$x$可能解析到同一个item。在实际环境中，这仅意味着碰撞的概率非零，且后续会通过放置算法回溯（见章节3.2.1）。

如果uniform bucket的大小改变，会发生device间的完整的数据重调配，这很像传统的基于哈希的分部策略。

3.4.2 list bucket

list bucket结构的内容被组织为一个链表，它能容纳任意权重的item。为了放置一份副本，CRUSH从保存着最近被添加的item的链头开始，将它的权重和其余所有的item的权重作比较。后续操作取决于$hash(x,r,item)$的值，或者会以适当的可能性选取当前的item，或者继续递归处理这个列表。这种源于RUSH_p的方法将放置的问题转化为“选择最近被添加的item还是之前的item？”。这对于扩展中的集群来说，是一个很自然且直观的选择：或者按适当的概率将对象重新定位到最新的device上，或者它像以前一样保留在旧的device上。在item被加入到bucket时，数据迁移是最优的。然而，当item从链表的中间或尾部移除，会导致大量的不必要的数据移动。因此list bucket最适合bucket从不（或很少）缩小的情况。

RUSH_p算法约等于包含内有许多uniform的单个list bucket的2层CRUSH结构。它因集群表示形式固定而无法使用放置规则或CRUSH中通过控制数据放置而增强可靠性的故障域。

3.4.3 tree bucket

像所有的链表数据结构一样，list bucket对于较小的item的集合效率很高，但是可能不适用于较大的集合，因为其$O(n)$的运行时间可能太大。而源于RUSH_T的tree bucket通过将它的item保存在二叉树中解决了这一问题。这将放置时间减小到了$O( \log n )$，使其适用于管理大得多的device或嵌套的bucket集合。RUSH_T等同于一个由包含许多uniform bucket的单个tree bucket的2层CRUSH结构。

tree bucket的结构为一个叶子为item的加权二分搜索树。每个内部节点都知道它左子树的总权值和右子树的总权值，且被打上了一个相应的固定策略的标签（后文中会讲解）。为了在一个bucket中选取一个item，CRUSH从树的根节点开始执行，它根据输入键$x$、副本编号$r$、bucket标识符、和当前树节点的标签（初始为根节点）计算哈希。其结果将与左右子树的权重比进行比较，以决定接下来访问哪个子节点。这一过程会反复执行直到到达叶子节点，该叶子节点相关的bucket中的item会被选择。在定位item时，仅需要$ \log n $次哈希运算和节点比较。

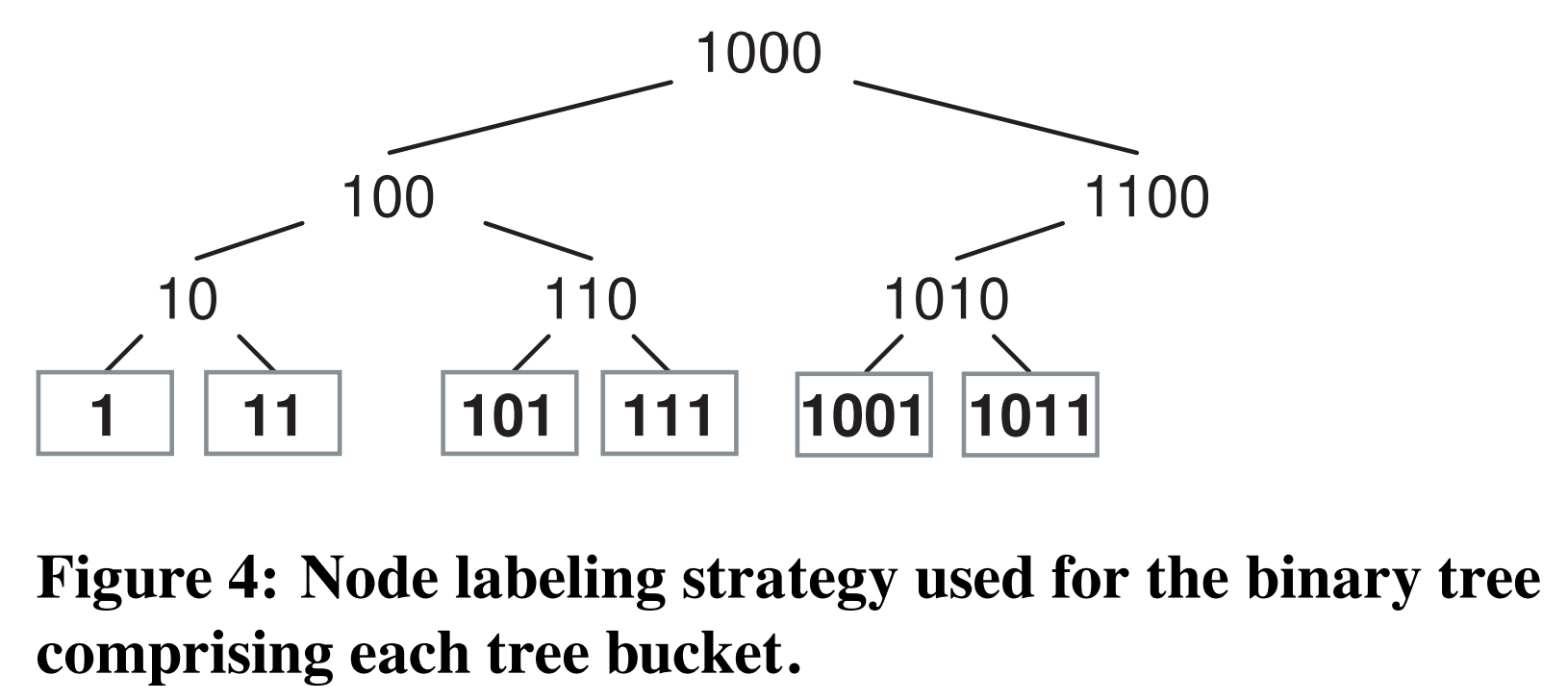
bucket的二叉树节点被打上了二进制值的标签，这使用了一个简单、固定的策略以避免当树增长或缩小时标签改变。数的最左叶子总被标记为“1”。每当树被扩展时，旧的根节点会变成新的根节点的左孩子，新的根节点被标记为旧的根节点的标签左移一位的值（1,10,100，等等）。树的右侧节点的标签是镜像，除了每个值前都加上了一个“1”^译注1。图4中展示了一个有6个叶子节点的带标签的二叉树。这一策略保证了当有新item被加入到bucket时（会从bucket移除时）或树增长时（或缩小时），对于任何已存在的叶子item，其穿过二叉树的路径仅需在开始放置决策树时向根节点添加（或移除）额外的节点。一旦一个对象被放置到了特定的子树时，它最后的映射将仅取决于权重和该子树中的节点标签，且只要子树的item不变就不会改变。尽管该层级决策树在内部item迁移时引入了一些额外的数据，这一策略能保证数据在合理的层级移动，同时即使在bucket非常大时也能提供高效的映射。

译注1：这里值前的“1”不是直接在右子树对应的左子树的节点的标签前添加一个“1”，“1”的位置取决于树扩展时新的根节点左移后的“1”的位置。例如，图4中根“10”扩展时，新的根为“100”，其右子树为“110”，右子树的左孩子叶子节点对应的左子树的标签为“1”，而新的根的“1”出现在第三位，因此第三个叶子节点的标签为“101”，以此类推。其实这只是一个用来维护搜索二叉树的二进制标签成立的简单算法。

3.4.4 straw bucket

list bucket和tree bucket的结构都需要计算有限数量的哈希值并与权重对比以选择bucket的一个item。为了提高副本放置的性能，它们都采用了某种分治方法，要么让某些item优先（例如，哪些在列表开始位置的item），要么根本不需要考虑item的整个子树。但是，在提高副本放置过程性能的同时，但也会在bucket的内容变更时（item的添加、移除、或修改item的权重）引入次优的重组织行为。

straw bucket在副本放置时能通过一种模拟抽签的方法让所有的item公平地“竞争”。在放置副本时，会向bucket中的每个item分配一个长度随机的签。签最长的item会胜利。每个签的长度最初是一个固定范围中的一个值，其基于CRUSH的输入$x$、副本编号$r$、和bucket item $i$的哈希得到。每个签的长度可通过一个基于其item的权重的因子$f( w_i )$伸缩^注3，因此权重更重的item更有可能赢得抽签，即$c(r,x)= \max _i ( f( w_i ) hash(x,r,i) )$。尽管这一过程几乎比list bucket慢两倍甚至比tree bucket（按对数伸缩）还要慢，但是straw bucekt能在变更时得到最优的内部item间的数据移动。

注3：尽管$f( w_i )$的简单解析解未知，但是程序化地计算权重因子是相对容易的（有源码）。该计算仅需要在每次bucket被修改时执行。

bucket的类型可根据期望的集群增长模式选择，在适当情况下可以用映射函数计算效率还换取数据移动效率。当期望bucket是固定的时（例如一个有相同磁盘的shelf），uniform bucket是最快的。如果bucket预期仅能够扩展，list bucket能在新item被加入到链头时提供最优的数据移动。这让CRUSH能恰好将适当的数据转移到新的device上，而不需要在其它的bucket item间调配数据。其缺点是映射速度为$O(n)$且当旧的item被移除或修改权重时会造成额外的数据移动。在可能存在item移除或重组效率很重要时（例如，接近存储层次结构的根处），straw bucket能在子树间提供最优的迁移行为。tree bucket是在各种方面折衷的方案，它能提供出色的性能和良好的重组效率。

4. 评估

CRUSH的设计基于很多种目标：均衡、在异构存储是被间加权分布、减小存储增加或移除时的数据移动（包括单个磁盘故障的情况）、通过跨多个故障域放置副本来提高系统可靠性、和迎来描述可用存储与数据分布的灵活地描述与规则系统。我们在相应的CRUSH配置下评估了这些行为，我们模拟了对象到device的分配并检验了分布结果，并与RUSH_P和RUSH_T风格的集群进行了对比。我们分别通过有1个包含了许多uniform bucket的list bucket或tree bucket的二层结构生成了RUSH_P和RUSH_T。尽管RUSH的固定的集群表示方式无法使用放置规则或跨故障域放置副本（CRUSH用此来提高数据安全性），但我们还是考虑了其性能和数据迁移行为。

4.1 数据分布

CRUSH的数据分布看上去应该是随机的（与对象标识符$x$或存储目标无关），且应在权重相同的device间形成均衡地分布。我们凭经验各种bucket类型的device间的对象分布，并比较了设备利用率与二项分布间的差异（二项分布是我们在理论上从完全均匀随机过程中得出的期望表现）。当我们分布$n$个对象且将每个对象放置在给定设备$i$上的概率是$ p = \frac{ w_i }{ W } $时，按相应的二项分布$b(n,p)$得到的设备利用率期望$ \mu = n p $，标准差$ \sigma = \sqrt{np(1-p)} $。在有许多device的大型系统中，我们可以近似$ 1-p \backsimeq 1 $，这样标准差$ \sigma \backsimeq \sqrt{ \mu } $——即使当数据对象的数量很多时，利用率也很高^注4:。正如期望的那样，我们发现对于由相同device组成的集群和不同权重的device组成的集群中，CRUSH的分布的均值与标准差始终与二项分布的相匹配。

注4：在有很多对象时（即当n很大时），二项分布近似于高斯分布。

4.1.1 过载保护

尽管CRUSH在有大量对象的情况实现了良好的均衡（设备利用率的方差小），但和任何随机过程一样，向任意的某个利用率明显大于均值的device分配对象的概率仍是非零的。不像已有的按概率的映射算法（包括RUSH），CRUSH有一个校正每个device复杂的机制，它可以重新分布一个device上任意比例的数据。这可以在device有过度使用的危险时，按比例缩小对该device的分配，来选择性地拉平过载device的负载。当向已用99%的容量的1000个device组成的集群分布数据时，我们发现尽管这导致了在47%的device上的负载调整，但是CRUSH映射执行时间的增长量却少于20%，且方差减小了4倍（正如预期的那样）。

4.1.2 差异和部分故障

之前的研究[Santos et al. 2000]表明随机的数据分布能让现实中的系统性能与精心的数据分条的性能相媲美（但稍慢一点）。在我们的自己的性能测试中，我们使用CRUSH作为分布式文件存储系统的一部分，我们发现随机对象放置会因OSD工作负载的差异而导致5%的写入性能下降，这与OSD利用率的差异程度有关。然而在实际环境下，这种差异大部分只会在精心设计的分条策略生效的同类工作负载下（通常是写入负载）才会出现。更常见的情况是，工作负载是混合的，且当它们到达磁盘时已经几乎是随机的了（或者至少与磁盘的布局无关），因此随机化测流和分条的策略在device负载和性能方面相似（尽管在精心设计的布局下也是如此），且都降低了差不多的整体吞吐量。我们发现在任何潜在的负载下，与CRUSH在元数据在分配的健壮性方面的缺失相比，其在少量工作负载下较少的性能损失就没那么重要了。

这一分析假设了随着时间变化device的能力几乎是静态的。然而，在真实系统中的经验表明，分布式存储系统的性能常常会被少量的缓慢的、过载的、碎片化的或性能差的device拖慢。传统的显式分配策略可以手动避免这类有问题的device，然而类哈希分布函数通常无法避免。CRUSH可以通过已有的过载校正机制来将这些表现不佳的device视为”部分故障“，从这些device上转移适量的数据和负载以避免这种性能瓶颈，并随着时间推移校正不均衡的负载。

正如DSPTF算法[Lumb et al. 2004]证明的那样，存储系统的细粒度的负载均衡能通过将读负载分摊到多个数据副本上来进一步减轻设备负载的差异。尽管这种方法与CRUSH互补，但是其不在CRUSH映射函数和本文的讨论范围内。

4.2 重组织和数据移动

我们在由7290个device的集群上对使用CRUSH和RUSH的系统在因新增或移除设备时导致的数据移动进行了评估。CRUSH集群深度有4层：9个row，每个row有9个cabinet，每个cabinet有9个shelf，每个shelf有10个device，总计7290个device。RUSH_P和RUSH_T等于一个2层CRUSH映射，它们分别包含单个tree bucket或list bucket，其下有729个uniform bucket，每个uniform bucket有10个device。其测量结果将与理论最优的数据迁移量$ m_{optimal} = \frac{ \Delta w }{ W } $进行对比，其中$ \Delta w $新增或移除的device的总权重，$W$是系统的总权重。例如，当系统容量加倍时，最优的重组织策略需要将半数的已有的数据迁移到新device上。

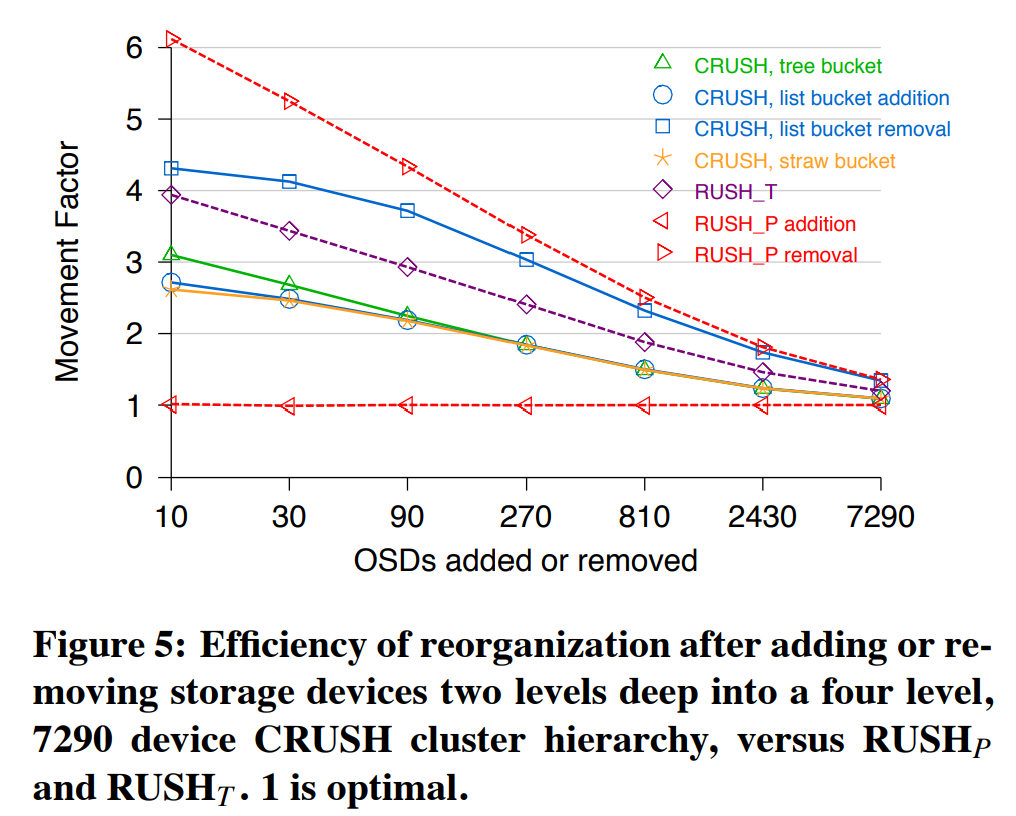
图5以移动因子$ m_{actual} / m_{optimal} $的性质展示了相对的重组织效率，其中1表示最优的对象数，越大的值意味着需要越多的移动。X轴是增加或移除的OSD的双，Y轴是移动因子的对数。在所有的情况下，更大的权重变换（与整个系统相比）会导致更高效的重组织。RUSH_P（单个大型list bucket）在极端情况下遥遥领先，即添加存储带来的移动最少（最优），而移除存储带来的移动最多（此时会有严重的性能下降，见章节4.3）。CRUSH中由list bucket（仅在只有存储添加的情况）或straw bucket组成的多层结构有次少的数据移动。使用tree bucket的CRUSH的效率稍微低一下，但是比朴素的RUSH_T好了几乎25%（由每个tree bucket中的9个item带来的轻微的的不均衡导致）。而正如预期的那样（见章节3.3），在由list bucket构建的CRUSH结构中移除存储的效率很差。

图6展示了在向不同类型的bucekt添加或移除内部item时的重组织效率。tree bucket变更的移动因子受二叉树的深度$ \log n $限制。向straw bucket和list bucket添加item几乎是最右的。uniform bucket的变更会导致整体数据的重调配。对链表尾部处的修改（例如移除最老的device）几乎会造成与bucket大小所占的比例相似的数据移动。尽管受这些限制，在整个存储结构中很少移除device时且要减小扩展带来的性能影响时，list bucket可能是合适的。结合了uniform bucket、list bucket、tree bucket和straw bucket的融合方法能在大多数常见的重组织场景下减小数据移动量，且仍能够维护良好的映射性能。

4.3 算法性能

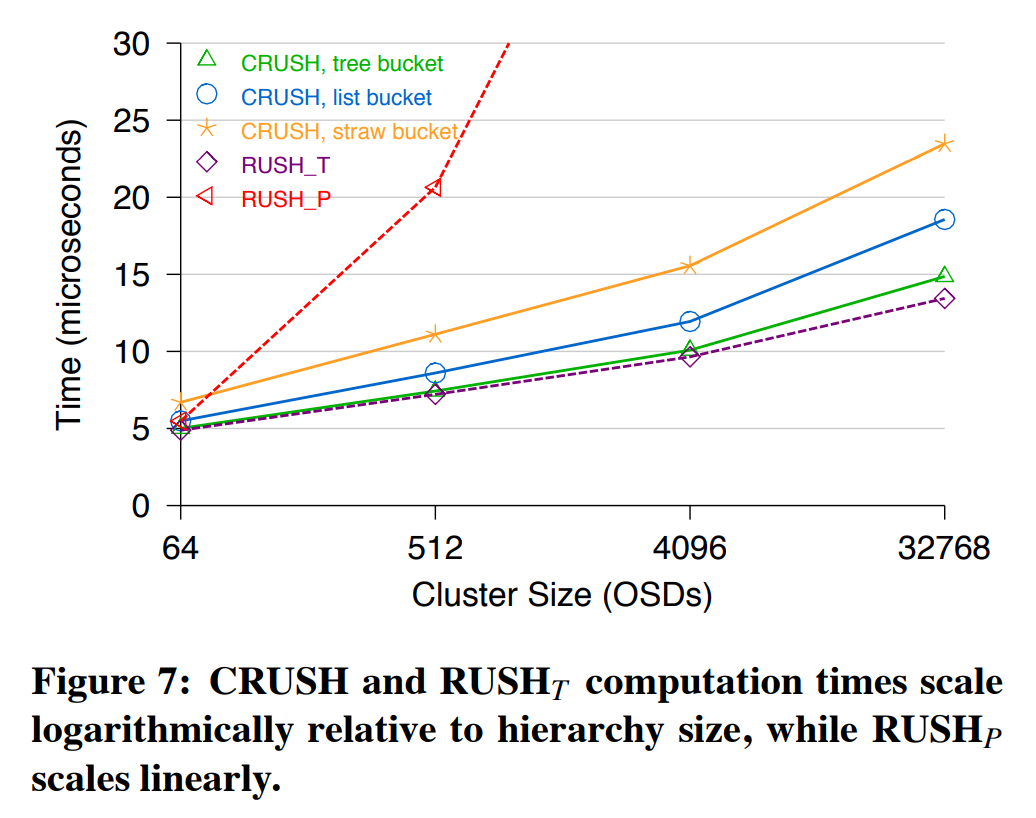
CRUSH映射的计算是为了快速而设计的，它能以$O( \log n )$计算n个OSD组成的集群的映射——因此devoce能够快速定位任何对象，或在集群映射变更后快速地重新评估它们已经保存了的对象的适当的存储目标。我们通过在不同大小的集群上的100万次映射检验了CRUSH的性能，并将其与RUSH_P和RUSH_T进行对比。图7展示了将一个副本集合映射到完全由8个item组成的tree bucket和uniform bucket的CRUSH集群（结构深度不同）的平均时间（ms），并与由固定的2层结构的RUSH进行对比。X轴是系统中device的数量，其坐标是对数的，因此它对应着存储结构的深度。CRUSH的性能与device的数量呈对数变化。RUSH_T的性能比CRUSH好一些，因为其稍稍简化了代码的复杂度。性能紧随其后的是list bucket和straw bucket。在本测试中RUSH_P是线性变化的（在32768个divice上消耗的时间比CRUSH长25倍），而在现实场景中，新部署的磁盘大小是随时间指数增长的，这会对其线性变化稍有改善 [Honicky and Miller 2004]。这些测试是在2.8GHz Pentium 4上进行的，总映射时间为数十微妙。

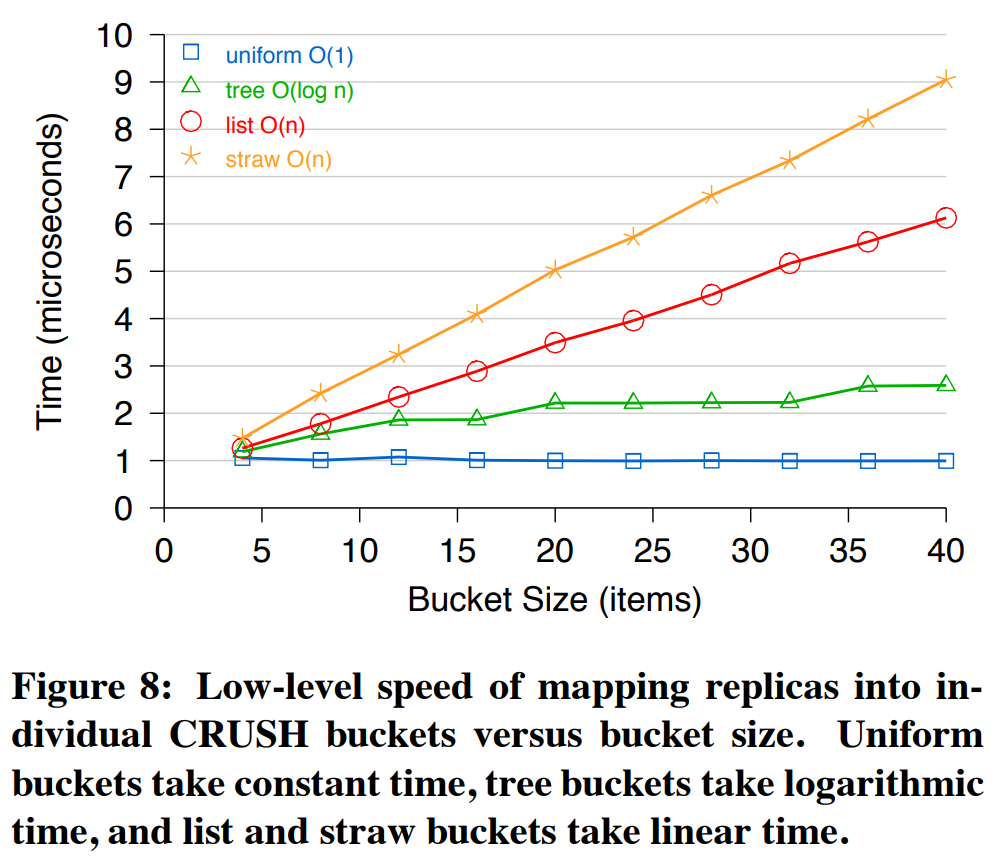
CRUSH的效率取决于存储结构的深度和其bucket的类型。图8比较了$c(r,x)$从每种类型的bucket中选取一个副本的时间（Y轴）作为bucket大小（X轴）的函数。在上层中，CRUSH按$O( \log n )$变化（即随结构深度线性变化），其每个bucket在不超过固定的最大大小下可能是$O(n)$的（list bucket和straw bucket线性变化）。不同的bucket类型在何时何处使用应取决于期望的新增、移除、权重修改的数量。list bucket提供了比straw bucket稍好一点的性能，然而在移除时可能导致过多的数据重调配。tree bucket在计算和重组织开销很客观的非常大或经常被修改的bucket中是一种很好的选择。

无论是执行时间还是结果的质量，CRUSH性能的核心来自于对整型哈希函数的使用。伪随机值是通过基于Jenkin的32位哈希混合[Jenkins 1997]的多输入整型哈希函数计算的。在目前的形式中，CRUSH映射函数的45%的时间都花费在了哈希值计算上，因此哈希是整体性能和分布质量的关键，它也是优化的重要目标。

4.3.1 被忽略的老化问题

CRUSH保留了故障的device在存储结构中的位置，因为通常故障时暂时的（故障设备通常会被替换）且这能够避免无效的数据重组织。如果忽略了存储系统的老化问题，发生故障但没被替换的deivce的数量可能会变得很大。尽管CRUSH会将数据重新分布到没有故障的device上，因为在放置算法中发生回溯的可能性变高了，它会带来少量的性能损失。我们在被标记为故障的device比例不同的1000个device组成的集群上评估了映射速度。在半数的设备故障的相对极端的场景下，映射计算时间增加了71%。（因为其现象是每个device的负载翻倍导致I/O性能的严重下降，所以这种情况很可能被这一现象掩盖。）

4.4 可靠性

对于大型存储系统来说，数据安全性是很重要的，因为设备数量大导致硬件故障的发生是很正常的。像CRUSH这种分簇分布的随机分布策略备受关注，因为它们扩大了与任意给定device共享数据的对等节点的数量。（通常来说，）有两个相互竞争且影响相反的因素。第一，因为副本数据更少的位能分布在更大的对等节点集合上，因此故障后的恢复能够并行执行，这减少了恢复时间且将系统的脆弱点的范围缩小到了其它故障上。第二，更大的对等节点的组意味着因同时发生了第二个故障而导致流丢失共享数据的可能性更高。在使用2路镜像时，这两个因素相互抵消；而在超过两份副本的情况下，数据的安全性随着分簇程度提高 [Xin et al. 2004]。

然而，多故障（multiple failure）情况的关键问题是：通常，故障可能不是独立的——在许多情况下，像电源故障或物理干扰这样的单个事件会影响到多个device，且采用分簇副本策略的更大型的对等节点组会增大数据丢失的可能性。CRUSH可将副本分散到用户定义的不同故障域中（在RUSH或已有的基于哈希的策略中都没有这一功能），这是专门为了防止并发的关联故障导致的数据丢失设计的。尽管这可以明显降低风险，但是缺少用来研究的特定的存储集群配置和相关的历史故障数据时，很难量化整个系统可靠性提高的程度。我们希望在以后进行这样的研究，但这超出了本文讨论的范围。

5. 展望

CRUSH正在作为Ceph的一部分进行开发，Ceph是一个数PB级的文件系统。目前的研究包括一个主要基于CRUSH的独有特性的智能、可靠的分布式对象存储。目前CRUSH使用的原始规则结构的复杂度刚好足以支持我们目前设想的数据分布策略。一些系统的特殊需求需要更强大的规则结构来满足。

尽管对意外故障发生时的安全性考虑是驱动CRUSH设计的主要目标，但是在可以用马尔可夫或其它定量模型评估其对系统平均数据丢失时间（MTTDL）的精确的影响前，还需要研究实际系统中的故障，以确定故障的特征与频率。

CRUSH的性能高度依赖于较为强大的多输入整型哈希函数。因为它同时影响着算法的正确性（分布的质量）与速度，因此，有必要对足以在CRUSH中使用的更快的哈希技术进行研究。

6. 结论

分布式存储系统对数据放置提出了一系列的独特的可扩展性的挑战。CRUSH通过将数据放置问题转化为伪随机映射函数解决了这些挑战，它消除了常见的元数据分配需求，转为通过基于用来描述可用存储的加权层次结构的方式分布数据。集群映射的层次接口能够反映出下层物理设备的组织情况和设施的基础架构情况，例如，在数据中心中，device被组成shelf、cabinet、和row，从而使自定义的放置规则可以定义各种策略以能够将对象的不同副本分布到不同的用户定义的故障域中（如不同的电力和网络基础设施中）。这样，CRUSH能够减轻通常在已有的采用分簇副本策略的伪随机系统中的关联设备故障问题带来的问题。CRUSH还通过选择性地将数据以最小计算代价地从装的太多的device迁出，解决了随机化的方法固有的设备中数据过量装载的风险。

CRUSH以极为高效的方式完成了所有这些任务，在计算效率和所需的元数据方面都是如此。映射计算的运行时间为$O( \log n )$，在数千台device的情况下执行时仅需几十毫秒。CRUSH集高效、可靠、灵活与一身，使其成为大型分布式存储系统的理想选择。

7. 致谢

R. J. Honicky’s excellent work on RUSH inspired the development of CRUSH. Discussions with Richard Golding, Theodore Wong, and the students and faculty of the Storage Systems Research Center were most helpful in motivating and refining the algorithm. This work was supported in part by Lawrence Livermore National Laboratory, Los Alamos National Laboratory, and Sandia National Laboratory under contract B520714. Sage Weil was supported in part by a fellowship from Lawrence Livermore National Laboratory. We would also like to thank the industrial sponsors of the SSRC, including Hewlett Packard Laboratories, IBM, Intel, Microsoft Research, Network Appliance, Onstor, Rocksoft, Symantec, and Yahoo.

8. 更多

CRUSH的源码采用LGPL协议，可通过https://users.soe.ucsc.edu/~sage/crush访问。

参考文献